Overview
1.Key insights On Scaling Laws for Reward Model Overoptimization
2.RM 相关 Scaling Law 研究设定
3.RM 不同参数规模下两种 Reward 的变化规律
4.RM 数据量 Scaling 的影响
5.RM 数据量的阈值效应
6.RL v.s BoN 的两个关键观察: KL 效率对比和 两类 reward 关联一致性
Key insights On Scaling Laws for Reward Model Overoptimization
1.古德哈特定律给我们的启示: 要关注指标过度优化/刷指标/Reward Hacking 问题:
When a measure becomes a target, it ceases to be a good measure. — Goodhart’s law
“当一个衡量指标变成了优化目标,它就不再是一个好的衡量指标” — 古德哈特定律
当我们想优化模型某个方面的能力的时候,这个能力就会被定义成一个指标,然后我们将模型朝着这个方向去努力的时候,我们做的是”刷指标”/“刷分”这种事情, 最终有可能和结果相反:
(i). 例如公司定义了一个 “客户满意度” 的指标, 这种指标的出发点是合理的—要提升满意度, 但是当客户满意度变成过度刷分的指标的时候,就会变得不合理,比如员工就会私下要求给好评,或者避开那种难以搞定的客户,最终反而是损害了用户的体验
(ii). 在 RLHF 领域同理,我们用一个 Reward Model 去代理人类的偏好, 如果我们过度关注 Reward Score,可能会学到人类表面喜欢的表达语气或句式,但整体生成的内容质量是下降的, 也就是发生 Reward Hacking
2.既然我们要关注 Reward Hacking 问题,那么就需要研究,Reward 优化过程随着优化规模的变化规律是什么?到什么程度范围内的优化是合理的?超过什么程度我们认为是 “过度优化的”? 简而言之,聚焦研究 Reward 的 Scaling Law 相关问题
RM 相关 Scaling Law 研究设定
1.我们聚焦研究随着 Reward Model 优化强度的增加,proxy Reward 的变化规律和 Gold Reward Score 的变化规律
2.首先固定一个 Gold Reward Model,这模型来自于一个人类真实偏好数据集训练出来的模型,这个模型在研究过程中不固定不变,该模型打出来的分数就是 Gold Reward
3.我们对比 Best-Of-N 和 RL 两种做法下的 Reward optimization 过程; 两种方式下对应的自变量都是模型优化的强度
(i). 在 RL 下我们采用 KL 作为自变量: 这里的 KL 的定于采取如下公式
表示 “新策略” 相对于 “初始策略” 的分布偏移程度
注意这里的式子和 PPO 经典损失公式中的 KL 项是不同的
PPO 经典损中的 KL 项是如下公式,核心目的是约束单轮策略更新的幅度,避免因为单轮更新幅度过大导致训练崩溃
(ii). 在 Best-of-N 这种方式下, 我们定义 KL 为一个 KL 散度解析计算式:
有必要理解下这个式子的定义
(a). 公式中的 n 代表候选序列的数量 N
(b). 通过该解析公式, 只要输入 n (候选序列的数量), 就能直接计算 BoN 策略与初始策略的 KL 散度,无需像 RL 那样采样大量轨迹,能大幅度降低计算成本
(c). 这个公式怎么来的? 有一个详细推导,晚点补充下, 我们可以先直接理解下这两项的意义
(d). 第一项 $\log n$ 是 KL 的主要贡献项, 代表了 BoN 选择数量 n 对于策略偏移的核心影响, n 越大偏移越多单调递增; 第二项是均匀性假设分布的修正项: $-\frac{n-1}{n}$, 我们先直觉上想一下这个式子 n = 1 修正为 0 说明无偏移; n = 2, 修正为 -0.5; n = 1000 的时候修正项约等于 -1, 这一项的本质是 “初始策略生成的候选序列并非完全均匀,存在微小的概率差异,因此需要对基础偏移量 $\log n$ 进行微调” ,确保公式在小 n 时的计算精度
RM 不同参数规模下两种 Reward 的变化规律
分别计算 RL 和 Best-of-N 两种策略下 [控制只有 RM 模型参数量变化],随着训练的进行/N的增加 KL 逐渐增大,proxy rm/gold rm score 的变化趋势是什么?
固定 policy 的模型参数是 1.2B
唯一变量是 RM 模型参数量 从 3M -> 3B
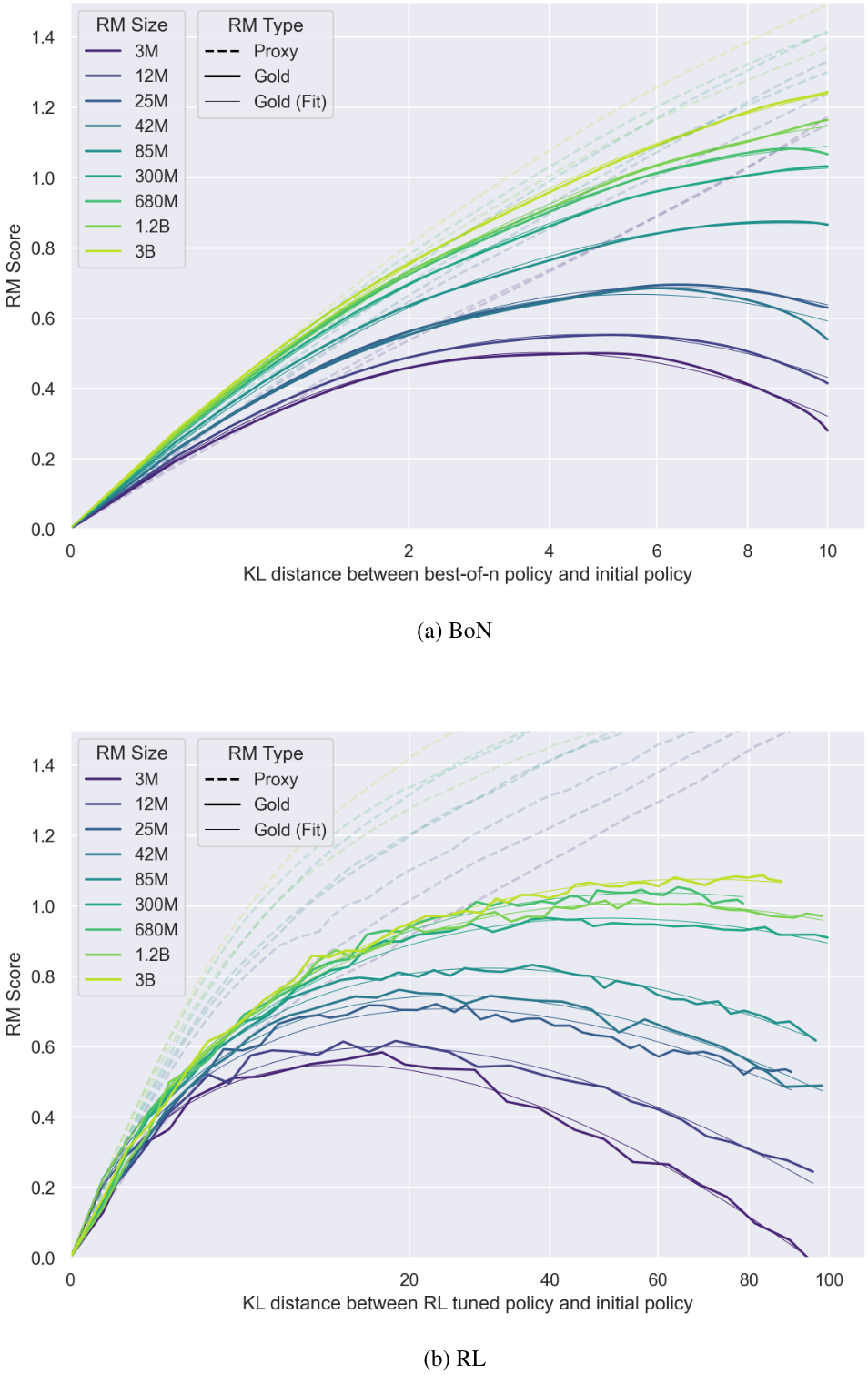
呈现出来的规律:
1.整体来看所有参数量的 RM,
一开始 proxy reward 和 gold reward 都很相关;但继续优化都会出现拐点,proxy reward 还在上升,但 gold reward 都开始下降
2.BoN 和 RL 这两种方法的趋势都保持一致
RM 数据量 Scaling 的影响


intuitively,
1.更多 RM 训练数据会带来两方面积极效果:
(i). 提升黄金分数 (Gold Score,代表真实偏好表现) .
(ii). 减少 Goodharting 现象 (即代理奖励偏离真实基准的过度优化问题),这一结果符合直觉,说明充足的数据能让 RM 更精准建模真实偏好,降低过优化风险
RM 数据量的阈值效应
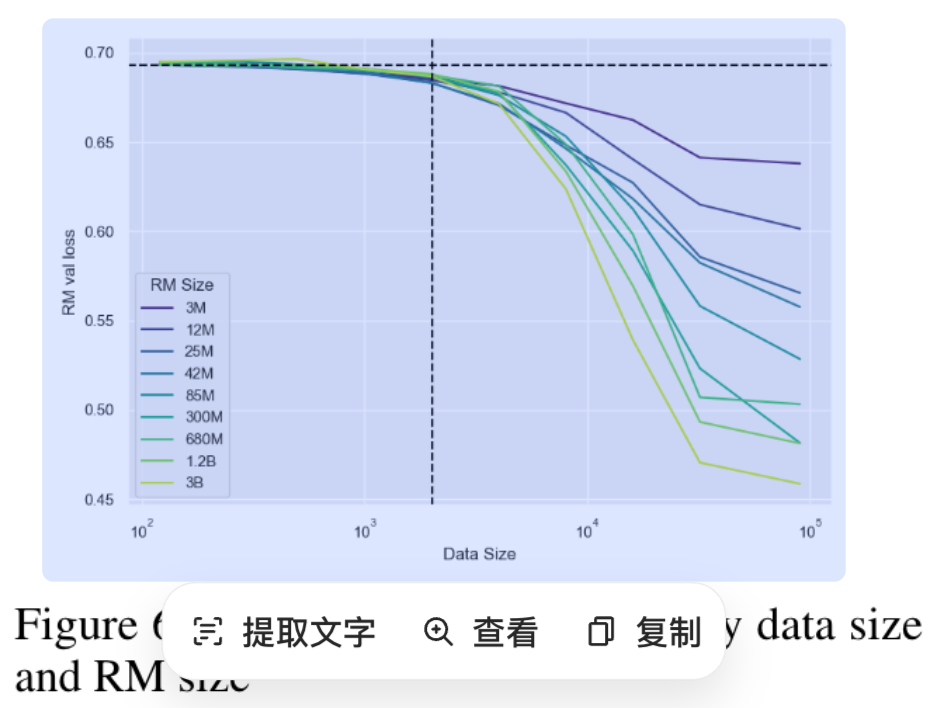
intuitively,
1.所有 RM 规模下均存在统一的数据量阈值 (约 2000 个对比样本) :
当 RM 训练数据量少于约 2000 个对比样本时,RM 的损失接近随机水平 (near-chance loss),几乎无性能提升 (Fig 6),且这一现象也反映在策略优化后的黄金分数如下图 (fig. 21)
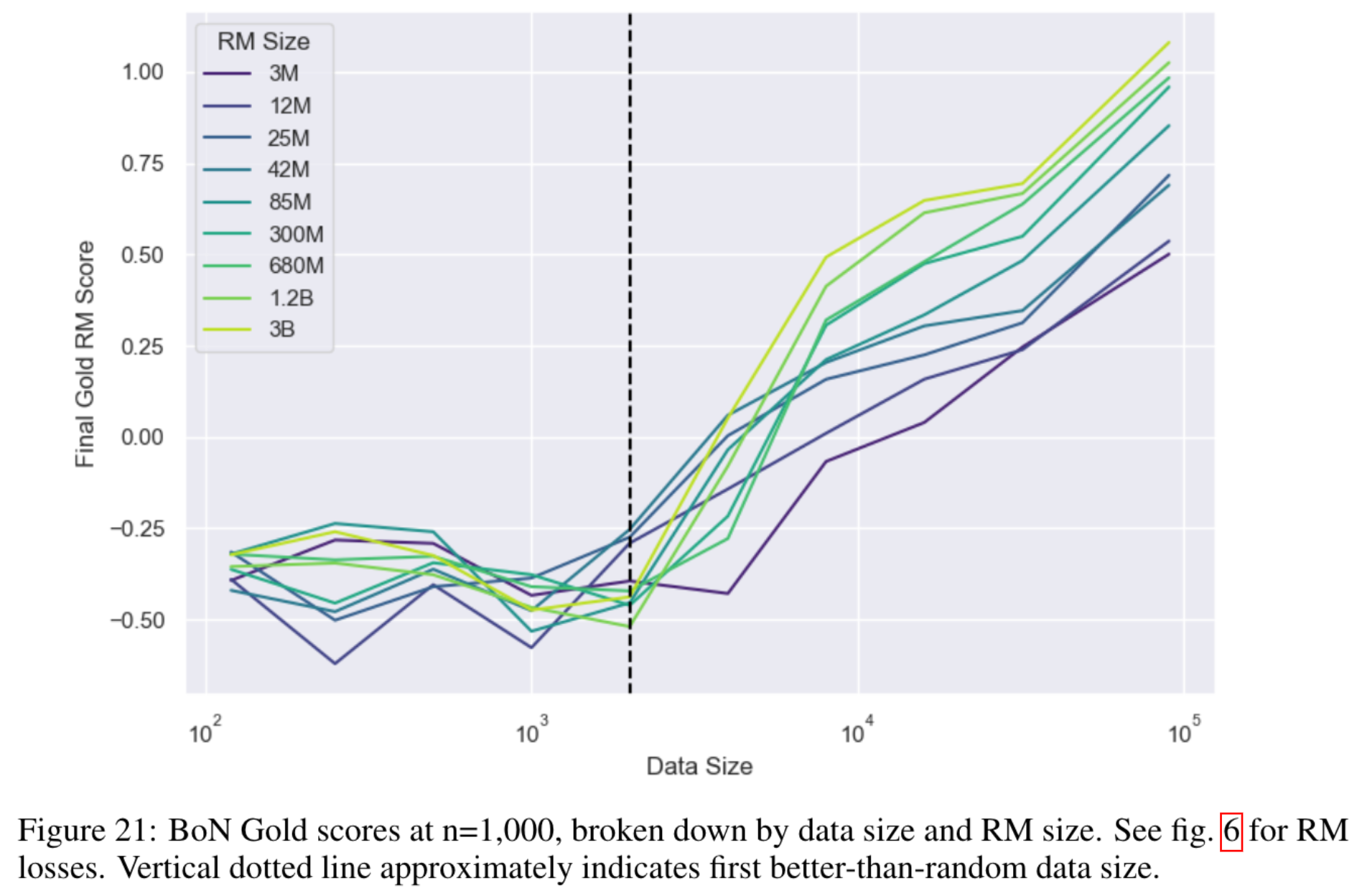
2.当数据量超过该阈值后,所有 RM 模型(无论后续提及的更大规模 RM)均会随数据量增加而性能提升,即黄金分数进一步改善,过优化风险进一步降低
RL v.s BoN 的两个关键观察: KL 效率对比和 两类 reward 关联一致性
RL is far less KL-efficient than BoN. Viewing KL distance as a resource to be spent, we observe that RL “consumes” far more KL than BoN. This means that both optimization and overoptimization require more KL to occur with RL. Intuitively, BoN searches very locally around the initial policy, and thus KLbon increases with roughly log(n). For RL on the other hand, each step modifies the
policy from the policy of the previous step—KL increases approximately quadratically with step in the absence of KL penalty (Figure 16, Figure 14). An implication of this result is that KL distance is an inadequate metric for quantity of (over) optimizationWhen looking at proxy vs gold RM scores, BoN and RL look more similar. The proxy RM score is another possible metric for quantity of optimization, because it is the value that is being directly optimized for. Using it as the metric of optimization leads to significantly more analogy between RL and BoN than KL distance does. However, we do observe that RL initially has a larger proxy-gold gap (i.e requires more proxy RM increase to match BoN), but then peaks at a higher gold RM score than BoN
intuitively,
1.我们首先定义一个概念 “KL效率”: 消耗单位 KL 的优化效果变化,也就是将 “KL 散度 (策略与初始策略的偏移程度)” 视为 “优化过程中消耗的资源”,KL 效率高意味着” 用更少的 KL 就能实现同等优化效果”
2.核心结论1: BoN 的 KL 效率远高于 RL RL 要实现”优化 (提升黄金奖励) “ 或”过优化 (黄金奖励下降) “,需要消耗比 BoN 多得多的 KL; 即相同 KL 下,BoN 的优化进度 (或过优化程度) 远快于 RL; BoN 其实实现的是 “初始策略局部搜索”:仅从初始策略 (SFT 模型) 生成的 n 个候选序列中选最优,策略偏移范围小,KL 随 n 的增长近似为对数关系 (log (n)) ; RL 实现的其实是 “迭代策略更新”:每一步都基于上一步的策略修改参数,若不施加 KL 惩罚,KL 随训练步数的增长近似为二次关系 (Figure 16、14 佐证) ,导致 KL 消耗速度远快于 BoN
3.核心结论2: 从对比 proxy reward 和 gold reward 的关联来看,RL 和 BoN 的优化趋势更相似: 打破了 “KL 指标下二者差异巨大” 的印象,说明 “以代理奖励为核心的优化逻辑” 是二者的底层共性,过优化的本质 (代理奖励偏离黄金奖励) 对两种方法一致
4.对 “算法选择 RL v.s BoN” 的启示:RL 与 BoN 各有优劣,需根据 “效率需求” 与 “性能目标” 做权衡:
(i). 若需 “快速优化、低 KL 消耗”:优先选 BoN (局部搜索效率高)
(ii). 若需 “更高真实偏好上限”:可选择 RL (虽 KL 消耗大,但最终黄金奖励峰值更高)
Reference
[1]. Scaling Laws for Reward Model Overoptimization.
转载请注明来源 goldandrabbit.github.io