Key Insight On ThinkRPM
1.我们想做一个 Step-level 的 verifier, 或者说目标是构建的 Process Reward Model (RPM, 过程奖励模型), 最高效的方法是什么? 蒸馏 Verification CoT
2.如果我们不做任何其他操作, 单纯利用推理模型以 LLM-as-a-judge 的方式做 process-level 的 verifier 的表现怎么样? 有很多问题: 评估稳定性不够, Overthinking, 格式不对,输出重复等
3.合成 verification CoT 数据,并用来做轻量微调, 得到 ThinkRPM: 带 CoT 的 Reasoning Model,能否提升模型作为 verifier 的能力? 提升显著
4.经过微调的 Process Reward Model (ThinkRPM) 对比 discriminative RPM 和原始采用 LLM-as-a-judge 的 verifier 的表现如何? 提升显著
LLM-as-a-judge 直接做 process-level verifier 的局限性
如果我们不做任何其他操作, 单纯找一个强大的推理模型,利用推理模型以 LLM-as-a-judge 的方式做 process-level 的 verifier 的表现怎么样? 如果效果已经很好那么我们就直接拿来用来做 verifier 完事了; 因此我们首先要验证下最直接的 LLM-as-a-judge 的方案的可行性; 但 3.1 章节实验从 prompt 和示例看并没有严格按照每个 step 生成 “yes/no” 去逐步验证结果,而是目标先生成一些 CoT 结果直接从中看出来一些这种方法天然的局限性
LLM-as-a-judge 生成 process-level verification 的具体流程:
1.数据集采用 OmniMath 和 OlympiadBench 是包含
2.模型采用 QwQ-32B-Preview 推理模型
然后在数据集上用 LLM-as-a-judge 的方式做 process-level verify, 评判过程每一步是不是正确的, 采用 的 prompt 模板如下, 该 prompt 写明了题目设定和解题过程 (放在 prefix里面), 然后一次性给定过程评估以及结果
输入: 题目和 prefix
输出: 每个步骤的评判以及最终的答案
The following is a math problem and a solution (split into steps, enclosed with tags and indexed from
0):
[Math Problem]
{problem}
[Solution]
{prefix}
Your task is to review and critique the solution step by step. Your output must be in the following format:
Step 0: <critique>
Step 1: <critique>
...
Step n: <critique>
After your analysis, return yes/no depending on whether the solution is correct.
Please put your final answer (i.e., yes/no) in \boxed{}
利用 QwQ-32B-Preview 模型给出来一个 step-level 的 verification, 注意这里没有评判 yes/no, 而是生成的是 critique 原文
Let’s verify step by step:
Step 0: The initial step seems to correctly identify the given information in the problem. It mentions
the quadrilateral ABCD with angles at B and D summing to 270◦, and the circumcircle of △ABD
intersecting CD at E, distinct from D. The lengths BC = 4, CE = 5, and DE = 7 are also noted.
This step is accurate in summarizing the problem statement.
Step 1: This step attempts to apply properties of cyclic quadrilaterals but seems to get confused about
the sum of angles in quadrilateral ABCD. It is mentioned that in a cyclic quadrilateral, opposite
angles sum to 180◦, but the given sum of angles ∠B and ∠D is 270◦, which indeed seems inconsistent.
However, the step then suggests assuming that one of the angles is 90◦ for the sake of explanation,
which is an adjustment to proceed with the solution. This part is a bit problematic because it alters the
given information, but perhaps there was a misinterpretation in the problem statement.
Step 2: Here, the Power of a Point Theorem is applied to points related to the circle. However, there is
confusion in calculating the length of CD. It states that CD = BC +CE = 4+5 = 9, but since E is a
point on CD distinct from D, and DE is given as 7, this suggests that CD = CE +DE = 5+7 = 12,
not 9. This is an error in calculation. Furthermore, the application of the Power of a Point Theorem
seems misapplied because E is on the circle, not outside it, so the theorem should be applied differently,
possibly considering intersecting chords.
Step 3: Recognizing the discrepancy in the previous step, the solution acknowledges the need for
reevaluation, which is a good practice. However, without correcting the earlier mistake in calculating
CD, the subsequent steps may be built on incorrect foundations.
Step 4: This step aims to find the diameter of the circumcircle of △ABD, which is the main goal of
the problem. It notes that the diameter is related to the circumradius, but without specific details about
the triangle’s sides or angles, it’s challenging to compute directly. The solution hints at the need for
more information, which is accurate.
Step 5: The insight here is that the relationship between E and the other points might provide the
necessary information through chord properties or trigonometric relationships. However, due to the
earlier discrepancies, this step does not lead to a concrete calculation.
Step 6: The conclusion reflects on the complexities and discrepancies in the problem and the solution
approach. It acknowledges that the direct calculation for the diameter is not straightforward with the given information, which is a fair assessment.
Overall, while the solution attempt shows an understanding of relevant geometric principles, there
are significant errors in calculation and application of theorems, particularly in Step 2. These errors
propagate through the subsequent steps, leading to an inconclusive solution. Therefore, the solution is
not correct.
\boxed{no}
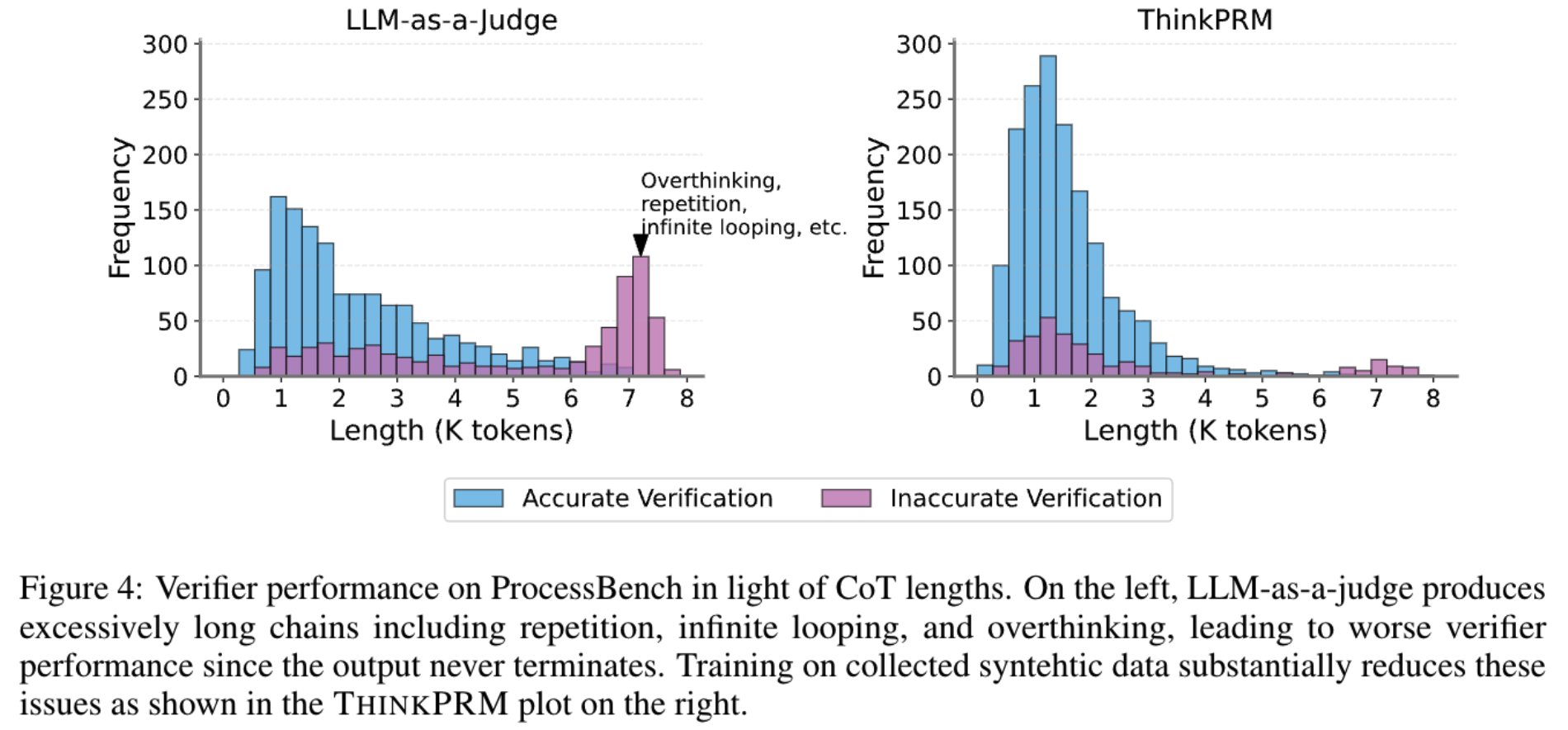
LLM-as-a-judge 的结果如下图左边所示, 图中的数值都是 F1-score, 红色的括号标记的是输出有问题率, 问题包括输出中有重复,无效label格式,过度思考等; 这里有个细节是 prompt 模板中并没有明确指令要求 step 输出 yes/no 这种标签,为什么能算 F1-score? 真令人感到困惑,猜测这里应该还是对 step-level 的 critique 有一步骤解析,生成 yes/no 标签再去统计的
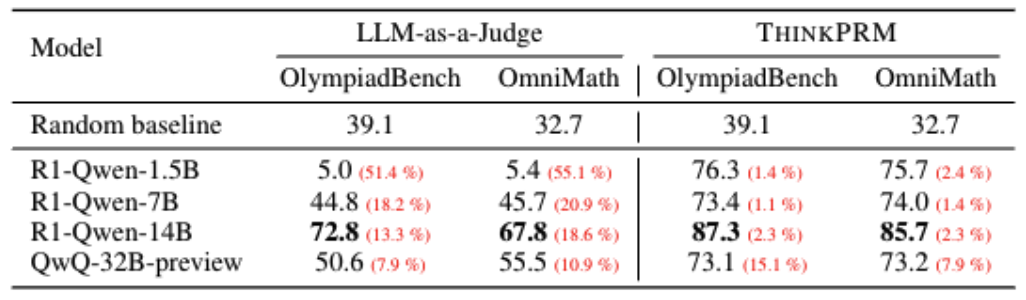
发现 LLM-as-a-judge 有如下的局限性:
1.LLM-as-a-judge 方法对于输入 instruct 内容敏感,只要我们稍微修改 instruct 的措辞,F1-score 都会发生 3-4 个点的变化; 这说明评判是不够稳定的
2.LLM-as-a-judge 生成 verification 有时候是无法解析格式的标签,(我感觉是你 prompt 写的有点问题不明确呢? 你的 prompt 都没加要明确输出 yes/no 这种输出呢)
3.LLM-as-a-judge 有时候会生成一些 Overthinking 的的 case,在 CoT token 有限制的情况下是不适配的 (题目步骤就算再长, 一个题目推理一次也解决不了吗? )
4.LLM-as-a-judge 有时候出现无限循环或者重复的情况 (这显然是模型本身能力不足的问题,也不能都怪 LLM-as-a-judge 这方法不行吧)
intuitively,
1.经过分析指向了直接用 LLM-as-a-judge 不够有效, 还需要得合成高质量 CoT 数据微调才有机会生成高质量的 Process Reward Model
ThinkRPM: 合成 verification CoT 微调提升 process verification 能力
既然直接 LLM-as-a-judge 有缺陷,那我们就合成高质量的 process-level verification 数据集, 然后训练一个更强的 step-level verification model, 且这个 model 集成很强的推理过程, 也就是 ThinkRPM 模型, 达到的效果是
ThinkRPM
输入: 对一个原始问题和问题多步解决过程
输出: 对每一步过程进行强力验证并准确判断该步骤是否正确
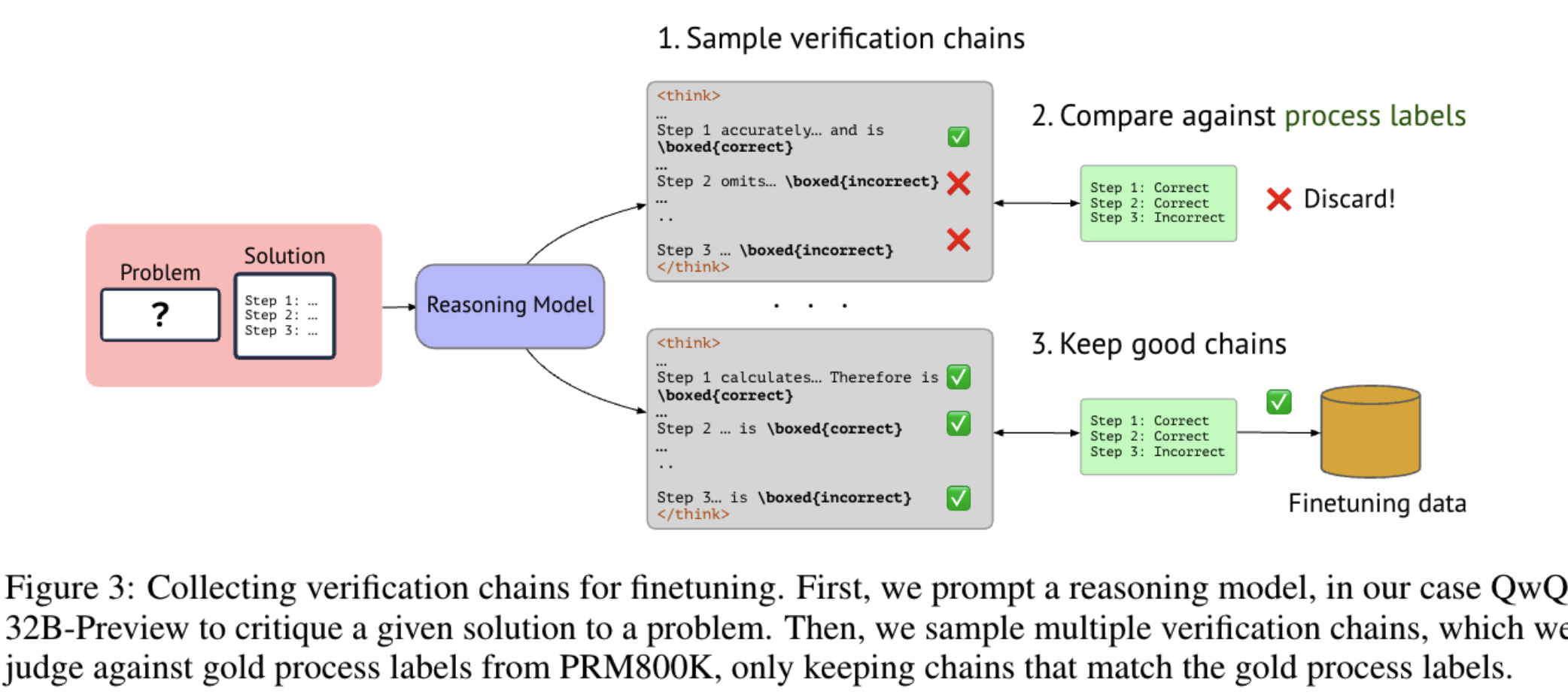
process-level verification 训练数据合成
生成推理仍然用 QwQ-32B-Preview 推理模型
训练数据集用 RPM800K 数据集, 这个数据集包含了问题的逐步过程和中间过程的 ground-truth 标签, 其中步骤中有的是正确有的是错误,如下所示
{
"problem": "Which of the following statements are true? A. 3 is a factor of 18. B. 17 is a divisor of 187 but not of 52. C. 24 is neither a divisor of 72 nor 67. D. 13 is a divisor of 26 but not of 52. E. 8 is a factor of 160.",
"ground_truth_answer": "A,B,E",
"steps": [
{"step": "A. 3 is a factor of 18.", "correct": true},
{"step": "B. 17 is a divisor of 187 but not of 52.", "correct": true},
{"step": "C. 24 is neither a divisor of 72 nor 67.", "correct": false},
{"step": "D. 13 is a divisor of 26 but not of 52.", "correct": false},
{"step": "E. 8 is a factor of 160.", "correct": true}
]
}
合成数据的指令如下: 这里就明确说明 “and determine whether each step is correct” (为什么之前不这么做?)
You are given a math problem and a proposed multiple-step solution (with a step on each line):
[Math Problem]
{problem}
[Solution]
{solution}
Review and critique the proposed solution steps and determine whether each step is correct.
If the solution is incomplete, only critique the steps that are provided. Your output must be in the following format:
Let’s verify step by step:
Step 1: <critique>...The step is \boxed{correct/incorrect}
Step 2: <critique>...The step is \boxed{correct/incorrect}
. . .
Step n: <critique>...The step is \boxed{correct/incorrect}
Once you find an incorrect step, you should stop since you don’t need to analyze the remaining steps.
process-level verification 训练数据后处理
得到 Verification CoT 之后, 我们还需要进行后处理筛选有效的 CoT verification:
1.格式约束: 每个步骤必须包含 \boxed{correct/incorrect} 这种标签
2.正确性约束: 与 ground-truth 对齐:每步生成的 step-level 正确与否判断必须和 PRM800K 数据集的 gold step labels 匹配
3.长度约束: CoT 长度不能超过最大的 budget
4.保留 1K CoT,对应 8K 个步骤标签
最终给出一个最终合成样本的示例
Problem: Find the area in square feet of a square with a perimeter of 32ft.
Solution:
Step 1: A square has four equal sides, so the perimeter is four times the length of one side.
Step 2: I can write an equation to relate the perimeter and the side length: 4s = 32, where s is the side
length in feet.
Step 3: To solve for s, I can divide both sides by 4: s = 32/4 = 8.
Step 4: Now I know the side length of the square is 8 feet.
Step 5: The area of a square is the side length squared, so the area is s² = 8² = 64.
Step 6: The area is in square feet, so the units are ft².
Step 7: The answer is 64 ft²
<think>
Alright, let’s verify step by step the solution provided for finding the area of a square with a perimeter
of 32 feet.
Step 1: "A square has four equal sides, so the perimeter is four times the length of one side."
Critique: This statement is accurate. A square indeed has four sides of equal length, and the perimeter
is the sum of all sides. Therefore, perimeter (P) equals 4 times the side length (s), or P = 4s.
The step is \\boxed{correct}
Step 2: "I can write an equation to relate the perimeter and the side length: 4s = 32, where s is the side
length in feet."
Critique: Given that the perimeter is 32 feet, setting up the equation 4s = 32 is correct. It properly
represents the relationship between the perimeter and the side length of the square.
The step is \\boxed{correct}
Step 3: "To solve for s, I can divide both sides by 4: s = 32/4 = 8."
Critique: This step correctly solves for s by dividing both sides of the equation by 4. The calculation 32
divided by 4 equals 8 is accurate.
The step is \\boxed{correct}
Step 4: "Now I know the side length of the square is 8 feet."
Critique: Based on the previous step, s = 8 feet, which is correctly stated here.
The step is \\boxed{correct}
Step 5: "The area of a square is the side length squared, so the area is s² = 8² = 64."
Critique: The formula for the area of a square is indeed s squared. Calculating 8 squared equals 64 is
correct.
The step is \\boxed{correct}
Step 6: "The area is in square feet, so the units are ft²."
Critique: Since the side length is in feet, the area will be in square feet (ft²). This is the correct unit for
area.
The step is \\boxed{correct}
Step 7: "The answer is 64 ft²"
Critique: This is the final answer, correctly stating the area as 64 square feet.
The step is \\boxed{correct}
</think>
Is the solution correct? Yes
实验细节对比
1.在训练 ThinkRPM 模型时, 基于多个模型 (QwQ-32B-preview/R1-Distill-Qwen{1.5B,7B,14B}) 比较在合成数据上微调的模型得到 ThinkRPM 和 原有的 LLM-as-a-judge 的结果, 发现 F1-score 显著比 LLM-as-a-judge 的结果好
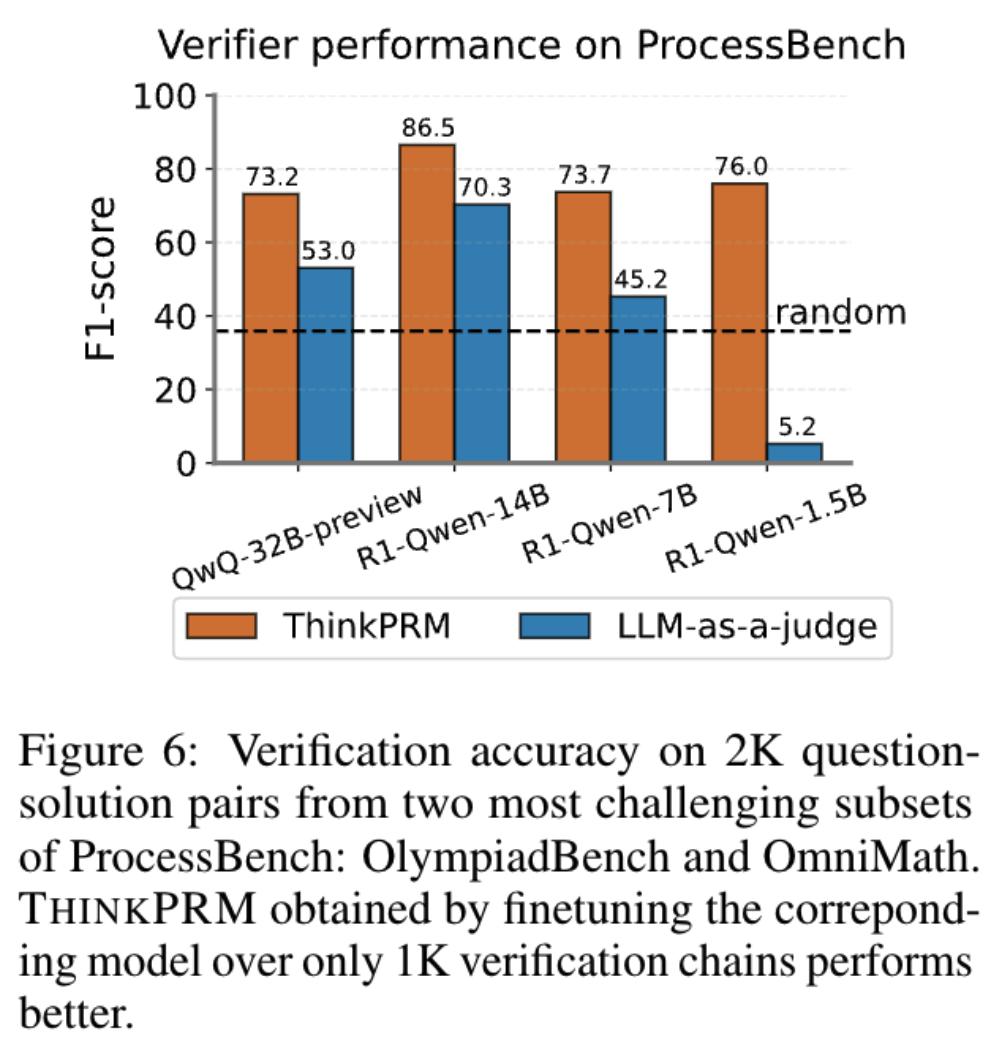
2.从生成 verification 长度分布来看,LLM-as-a-judge 会经常出现各种重复问题、无限循环问题或者 overthinking 问题, 但是 ThinkRPM 明显得到了缓解
Reference
[1]. Process Reward Models That Think.
转载请注明来源 goldandrabbit.github.io