Shepherd: noun: 引导者/指导者/牧羊人, verb: 带领/领导/指导/看管
Key Insight On Math-Shepherd
1.采用 MCTS (蒙特卡洛树搜索) 思想实现自动 Process-level Reward 过程奖励标注, 即对当前的 step 实现评分
2.融合 self-consistency 和 process reward model 来验证 PRM 有效性并选择高质量推理路径 for RL
MCTS 自动过程标注
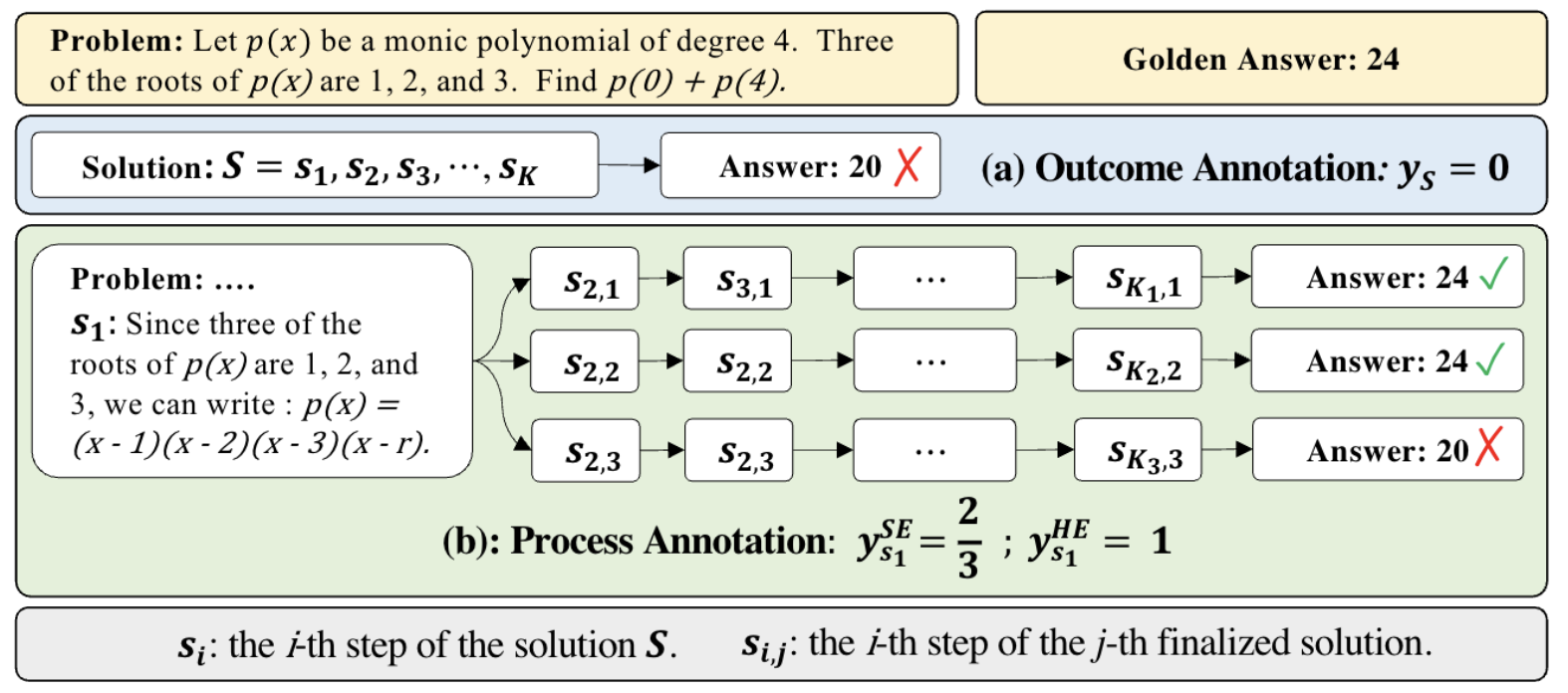
类比 MCTS 的过程, 我们生成自动过程标注的过程分为 Completion 和 Estimation 两个步骤:
1.Completion 生成 $N$ 条候选序列: 对于一个问题 $p$, 用一个 completer 去补全总共 $N$ 个子推理序列, 序列的 index 用 $j$ 来表示, 每个序列中都会产生一系列的 step, step 的 index 用 $i$ 表示
2.Estimation 量化步骤 $si$ 的价值 $y{s_i}$, $s_i$ 基于从它开始生成的所有可能完成的序列, $s_i$ 通向未来的结局有多种, 可能有的正确, 可能的错误, 我们关心的是一个 “潜力评分” 或者 “未来的可行性”, 计算上有两类方法 hard_estimation 和 soft_estimation:
(i). hard estimation 的想法: 只要 $s_i$ 步骤到末尾有一次能推理出来最终的答案是正确的, 那么就是一个对的结果给 1 分
(ii). soft estimation 的想法: 从 $s_i$ 能走的全部路径来看, 在所有的路径上算个平均的 step level 的分数
举个例子:计算 7×6+5, 对中间步骤 $s_i$, 我们采样生成 $N=5$ 条序列如下:
| 序列 j | 模拟 step | 最终答案 |
|---|---|---|
| 1 | s_i → +5 | 47 |
| 2 | s_i → +4 | 46 |
| 3 | s_i → +5 | 47 |
| 4 | s_i → +5 | 47 |
| 5 | s_i → -1 | 41 |
3.想一下为什么这样标注 reward 有合理性?
估计一个步骤的价值, 本质上就是做 MonteCarlo 的思想, 用这些序列最终的表现来估计 $s_i$ 的价值, 也和 RL 中的 value function 的思想类似, 估计的是状态的潜在价值
4.训练 RPM 模型
基于如上两步, 我们生成了推理路径的过程标注数据, 然后就能利用过程标注数据训练一个 RPM 模型, 也就是 step-level 的公式
Ranking for Verification 验证 MCTS-based process reward 的有效性
1.那如何验证我们这种自动过程标注的 reward 是不是准确呢?我们手上其实目前就两个东西, 一个是最终的答案的 ground truth, 另一个就是我们这种 step level 的打分; 因此我们只要基于 step-level 的打分构造一个 sequence-level 的打分以及对应的答案, 那么和 ground truth 对照一下一致性, 就可以初步验证有效性了: 如果通过 Ranking for Verification 策略选出的最终答案与 ground truth 一致率高, 说明我们的 PRM + MCTS 计算出的 reward 是有效的, 可用于 RL 优化的
2.如果有了很准确的 process reward model, 也能够基于 verification 策略用作 RL 过程中的高质量轨迹筛选
3.已有 step-level 的评分, 再评估一个 sequence-level 序列粒度的打分就不难了, 有两种方法:
(i). Minimum Score (最小值策略): 用序列中所有步骤的最小分数作为序列的分数, 背后的直觉是: 如果有哪一步非常不可靠/发生明确的错误, 整个序列的分数都会被拉低, 使得整个序列分数不会高于这个分数, 有点木桶原理的, 这种策略下序列价值估计是准确却最保守的
基于这种策略, 我们可以看下答案分数的分布和推理出的答案的分布是否是高相关性的
(ii). 融合 self-consistency + rm 的分数
RPM 的打分存在一个问题:某些 step 可能很高但是通向错误答案, 多条路径中可能某些答案压根就是错误的, 因此验证路径和答案的一致性或者自洽性非常重要; 我们可以先把所有的序列按照答案结果进行分组, 然后再组内进行聚合, 聚合的方式采用 RM score 求和, 兼顾了自洽性 (SC) 和质量 (RM) 两个因素, 公式如下:
其中 $S_i$ 是问题 $p$ 打出来的 ORM 或者 PRM 分数
这个公式的理解是:对每个组进行聚合算 rm score 和, 找到 rm score 和最大的那个那个组对应的答案, 作为真正的答案: 举个例子: 计算 7×5+7 有 $N=5$ 条序列, 最终答案与 PRM 分数如下
| 序列 | 最终答案 $a_i$ | RM 分数 |
|---|---|---|
| S1 | 42 | 0.9 |
| S2 | 47 | 0.4 |
| S3 | 42 | 0.8 |
| S4 | 47 | 0.5 |
| S5 | 42 | 0.7 |
按答案分组求和:
选择最高分: $a_1=42$
Reference
[1]. Math-Shepherd: Verify and Reinforce LLMs Step-by-Step Without Human Annotations
转载请注明来源 goldandrabbit.github.io