Key Insights On Inference with the Judgment Distribution
1.LLM-as-a-judge: 采用贪婪解码的方式效果不如利用 judge 分布取分布下的均值/期望的方式, 即基于概率分布取 Mean 是最优方法
2.LLM-as-a-judge: 对比 pointwise/pairwise scoring/pairwise ranking
3.LLM-as-a-judge: 对比 cot v.s non-cot,non-cot 更优优势
4.LLM-as-a-judge: 最佳实践总结
LLM-as-a-judge: Mean > Mode (Greedy Decoding)
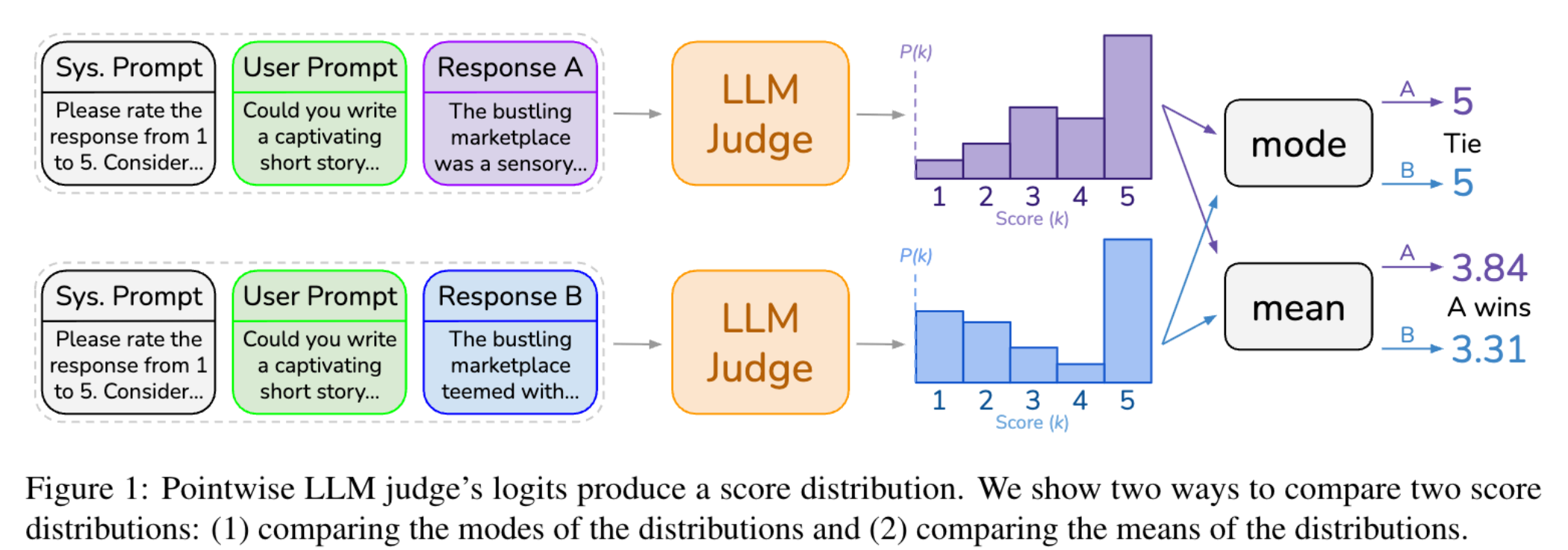
从最简单的 LLM-as-a-judge case 说起, 假设我们有个 LLM-as-a-judge 的 pointwise 的打分, 对应的 prompt 如下:
[System] You are a helpful and fair evaluator.
[User] Rate the following answer from 1 to 5.
Answer: ...
[Assistant] Rating:
通常我们用模型评分作为最终的评判结果, 因为 LLM 采用 greedy decoding 范式输出 softmax 最大概率的 token,所以等同于 mode 取众数等同于 greedy decoding
但我们可以进一步利用评级的分布信息计算更稳定的评分结果的,最简单的方法,我们对每种分类取 logit, 然后对概率分布加权求和取一个期望/均值, 得到的评分会更加的稳定和准确
具体来说对 5 个分类取 logits, 然后再通过 softmax 得到对应的概率 (分布)
| token | logit | softmax 概率 |
|---|---|---|
| 1 | -1.1 | 0.0370 |
| 2 | -0.3 | 0.0823 |
| 3 | 0.5 | 0.1831 |
| 4 | 1.4 | 0.4503 |
| 5 | 0.8 | 0.2473 |
Recap下 logit 怎么取的, 回顾下模型的结构
embedding
=> transformer blocks
=> final hidden state
=> linear projection (to vocab size)
=> softmax
=> token probabilities
模型的最后一层是一个线性层
其中, logits 层维度 == 词表的大小, 如下代码给出一个参考实现
from transformers import AutoModelForCausalLM, AutoTokenizer
import torch
model = AutoModelForCausalLM.from_pretrained("gpt-4o-mini")
tokenizer = AutoTokenizer.from_pretrained("gpt-4o-mini")
prompt = "Rate the answer from 1 to 5.\nAnswer: ...\nRating:"
inputs = tokenizer(prompt, return_tensors="pt")
with torch.no_grad():
outputs = model(**inputs)
# 我们要取出的东西: shape == [batch, seq_len, vocab_size]
# 这里 shape == [1, seq_len, vocab_size]
logits = outputs.logits
## 取最后一个 token 的 logits 分布
logits_last = logits[0, -1, :] # 对应 "Rating:" 之后要预测的那个 token
# 只挑选 token 分别为 "1"/"2"/"3"/"4"/"5" 对应的 logits, 忽略其他的
score_tokens = [tokenizer.encode(str(i), add_special_tokens=False)[0] for i in range(1,6)]
score_logits = logits_last[score_tokens]
# 手动算下 softmax
probs = torch.softmax(score_logits, dim=-1)
下面用代码模拟下分数输出
import torch
import torch.nn.functional as F
logits = torch.tensor([-1.1, -0.3, 0.5, 1.4, 0.8])
probs = F.softmax(logits, dim=0)
# 众数
mode_score = torch.argmax(probs).item() + 1 # token "1" 对应评分1
# 均值
mean_score = torch.sum(probs * torch.tensor([1,2,3,4,5])).item()
print("Mode score:", mode_score)
print("Mean score:", mean_score)
输出结果
Mode score: 4
Mean score: 3.79 # 均值分数对于分布刻画有更强的作用
Mean 为什么比 Mode (Greedy Decoding) 要更好 ?
1.在不同的实验配置 (pointwise scoring/pairwise scoring/pairwise ranking) 里面, mean 方法整体比 mode 准确率更高
对比 Mean 和 Mode 的效果结果如下,同时增加对比是否带 cot 在 Mean/Mode 模式的效果
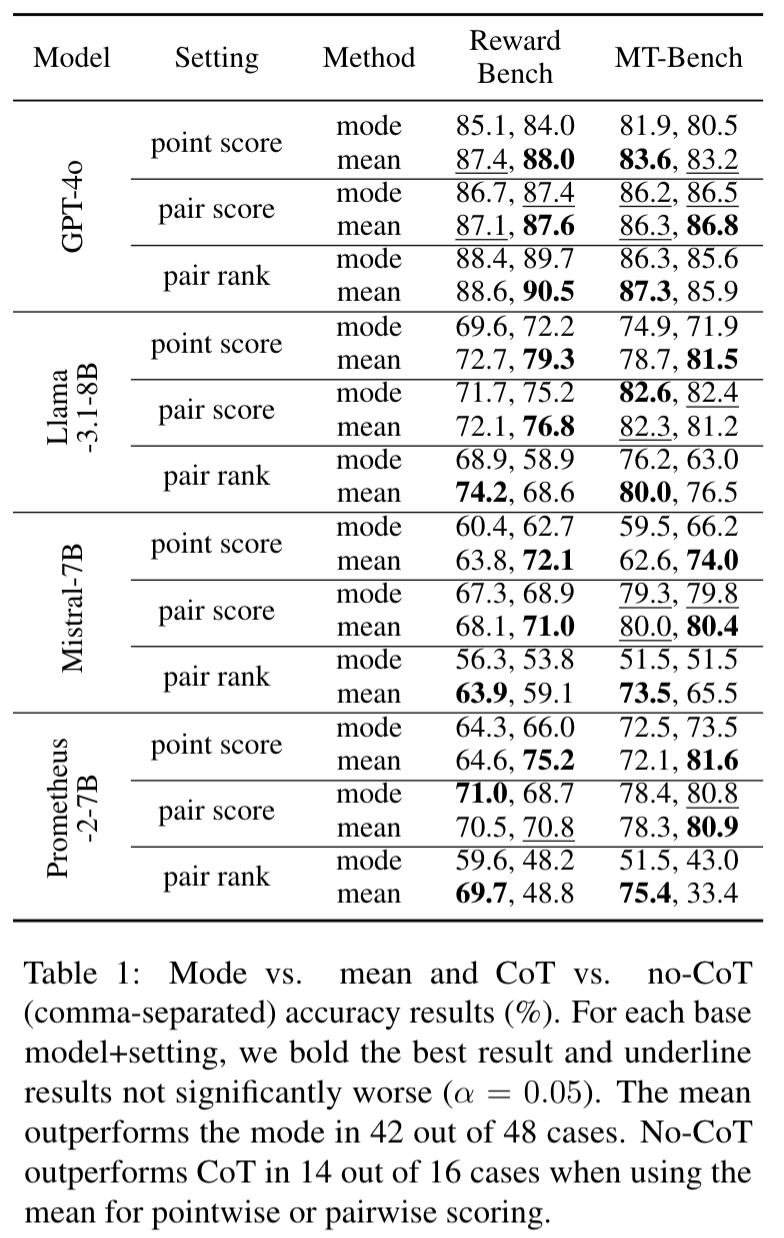
Mean outperforms mode The mean outperforms the mode in 42 out of 48 cases. In Table 10, we provide a subset breakdown of RewardBench and observe particularly large gains for pointwise scoring on the Reasoning subset.
We interpret the harmful effect of CoT on pointwise scoring with the smaller models as being due to sharpening, whereby the initial entropy in the judgment is lost as the model commits to one instantiation of a reasoning trace.
CoT often harms LLM-as-a-judge For the scoring settings, no-CoT outperforms CoT in 14 out of 16 cases when using the mean. We interpret the harmful effect of CoT on point-
wise scoring with the smaller models as being due to sharpening, whereby the initial entropy in the judgment is lost as the model commits to one instantiation of a reasoning trace.
intuitively,
(i).发现采用 cot-prompting 时,模型打分分布会变得更加 “尖锐/低熵”, 趋于集中
2.从分布理解上看
(i). 取 Mode 方法粒度更 “粗糙”, 分布里面多个分支概率接近,容易出现 tie; 或者会忽略掉分布的 “倾斜趋势”
(ii). mean 方法考虑了所有可能的值和概率,更能体现分布的中心趋势
LLM-as-a-judge: pointwise scoring v.s. pairwise scoring v.s pairwise ranking
LLM-as-a-judge 通常有三种方式 pointwise scoring v.s. pairwise scoring v.s pairwise ranking
Pointwise scoring
pointwise scoring: 通用 prompt 对单独答案采用 1-9 制打分,然后按照上面 mean 的方法来计算 score, 如下是两个 pointwise LLM-as-a-judge prompt (cot/non-cot):
## cot pointwise prompting
Please act as an impartial judge and evaluate the quality of the response provided by an AI assistant to the user prompt displayed below. Your evaluation should consider factors such as the helpfulness, relevance, accuracy, depth, creativity, level of detail, and ethicality of the response. **Begin your evaluation by providing a short explanation.** Be as objective as possible. **After providing your explanation**, please rate the response with an integer score from 1 to 9, without further explanation
## non-cot pointwise prompting
Please act as an impartial judge and evaluate the quality of the response provided by an AI assistant to the user prompt displayed below. Your evaluation should consider factors such as the helpfulness, relevance, accuracy, depth, creativity, level of detail, and ethicality of the response. Be as objective as possible. Please rate the response with an integer score from 1 to 9, without further explanation.
[User Prompt]
{User Prompt}
[End User Prompt]
[Start of Assistant's Answer]
{Assistant's Answer}
[End of Assistant's Answer]
Pairwise Scoring 配对同时评分
1.Pairwise Scoring (配对同时评分法) 是在同一个评分标准下 (上文 prompt 核心内容通常相同:任务说明、评分标准不变),同时输入两个答案 (例如答案 A 和答案 B), 然后完成 A 和 B 的打分
2.在实施层面通常会做 position-bias 消偏处理, 即对一个 pair 调转顺序打两次, 然后取各自的平均; 举个例子:
第一次打分 s1
请对以下两条文本评分(0~1分),并说明评分理由:
Text 1: 我喜欢猫
Text 2: 我喜欢狗
第二次打分 s2
请对以下两条文本评分(0~1分),并说明评分理由:
Text 1: 我喜欢狗
Text 2: 我喜欢猫
然后取平均下
s(“我喜欢狗”)=(s1(“我喜欢狗”)+s2(“我喜欢狗”))/2.0
s(“我喜欢猫”)=(s1(“我喜欢猫”)+s2(“我喜欢猫”))/2.0 .
Pariwise Ranking 偏序打分
Pairwise Ranking 的目标和 Pairwise Scoring 有所区别,Pairwise Ranking 的目标是严格对比两个答案, Pairwise Ranking 的打分流程:
输入:prompt + 两个答案, 要求输出偏序关系, 这里偏好关系定义为 5 类 token:
tokens = ["[[>>]]", "[[>]]", "[[=]]", "[<]]", "[[<<]]"]
输出:从五种偏序关系选择出来的 token
Please act as an impartial judge and evaluate the quality of the responses provided by two AI assistants to the user prompt displayed below. Your evaluation should consider factors such as the helpfulness, relevance, and informativeness of each response. Use the following symbols to indicate your judgment:
- "[[>>]]" if assistant A is significantly better,
- "[[>]]" if assistant A is slightly better,
- "[[=]]" for a tie,
- "[[<]]" if assistant B is slightly better,
- "[[<<]]" if assistant B is significantly better.
[User Prompt]
{User Prompt}
[End User Prompt]
[Start of Assistant A's Answer]
{Assistant A's Answer}
[End of Assistant A's Answer]
[Start of Assistant B's Answer]
{Assistant B's Answer}
[End of Assistant B's Answer]
然后让计算上面五个偏序 token 的 logit, 然后 softmax 得到概率分布
logits = model(prompt_tokens)
| symbol | probability |
|---|---|
| [[>>]] | 0.4 |
| [[>]] | 0.2 |
| [[=]] | 0.1 |
| [[<]] | 0.2 |
| [[<<]] | 0.1 |
然后 pairwise 的 score 是前三种的加权和, 其中相等偏序的 weight = 0.5:
Pairwise Ranking 得到案 A 比 答案 B 好的概率
对比 pointwise scoring v.s. pairwise scoring v.s pairwise ranking 对比
这三种方法有必要比较下优劣:
1.pointwise scoring 是最简单的做法, 但分数存在显著的校准问题, 不同候选文本之间的分数不保证直接可比;如果面向需求是构造 RM 的样本不可用
2.pairwise scoring 保证两条结果是有可比性的,缺点是因位置消偏还需要引入多一次推理
3.pairwise ranking 目标就是衡量两个对比的结果,具备最高的对比稳定性; 同时相比 pairwise scoring 得到的结果更能够满足 RM 样本的要求
4.如果任务是偏向于主观任务,pairwise ranking 的方式是最合理的, 比如比较那个答案更有创意,文笔更好;如果任务是客观的(例如,判断一个回答是否忠实于原文,或者是否包含不当内容),那么 pairwise scoring 或直接评分可能更合适,因为这里 “对” 与 “错” 的界限相对清晰
LLM-as-a-judge 的最佳实践
本 paper 的实验结果给出 LLM-as-a-judge 最佳实践:
1.基础范式: paiwise ranking 范式 + 均值打分处理 + non-cot 模式
2.cot 需慎重使用,因为 cot 的使用可能会带来熵变化的问题
3.永远处理 position-bias: 同一个 pair 永远要对比两次
4.pairwise scoring: 也是很有效的一种方法
Reference
[1]. Improving LLM-as-a-Judge Inference with the Judgment Distribution.
转载请注明来源 goldandrabbit.github.io