G&R Blog Release Regulation

Motivation

1.提出一种 CTR 模型中解耦校准能力和排序能力的损失: 将原本 1 个自由度的 logit 改成 2 个自由度的 logit 作差的形式
2.提出同时优化校准和排序的损失函数 (注意这里的校准和业务通常 CTR 校准不是一个概念, 目标和通常意义下的二分类排序损失 + LTR 损失联合建模更接近)

Two types of capabilities that CTR/CVR needs to have 点击率/转化率模型需要的两类能力

1.CTR 模型需要兼备两种能力, 1 个是校准能力 (calibration ability) 另 1 个是 (ranking ability), 其中校准能力可以写成下面的式子
2.注意这里的校准不是业务指标通常意义上的校准, 业务通常意义上的校准能力是 pcoc/calN/ECE 上的保证, 这里的校准指的仍然是做二分类排序能力; 为什么这里叫做校准? 因为本文要引出 LTR 的排序能力对模型效果的收益, LTR 的排序能力在这里用了 ranking ability, 相对本文研究的 ranking ability, 原始的二分类排序的能力称之为校准能力

$$\mathcal l_{\text{calib}}=-\sum_{x,y}\log\ \hat p(y|x)=-\sum_{x,y}\log\frac{\exp(f_\theta(x))}{1+\exp(f_{\theta}(x))}=-\sum_{x,y}\log\frac{1}{1+\exp(-f_{\theta}(x))}$$

如果这 2 种能力我们同时想要应该怎么做 ? 一种直接的思路就是融合这 2 个 loss , 但是直觉上这 2 种 loss 直接相加是不合理的

Joint Optimization of Ranking and Calibration 排序和校准同时优化

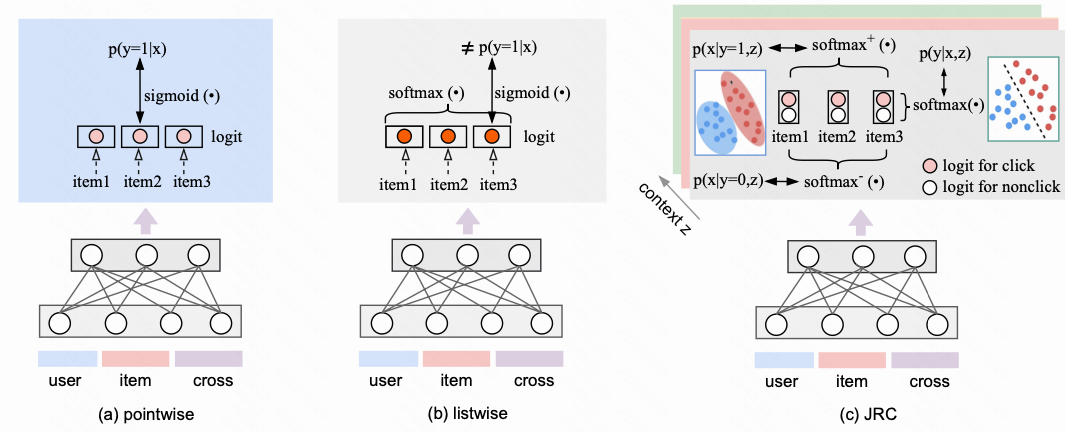
The intuition of introducing an additional degree of freedom is to alleviate the conflict between the optimization of ranking and calibration.

To avoid representing different meanings with the same logit, the proposed JRC extends the output logit from 1 dimension to 2 dimensions, $f:\mathbb R^{D}\rightarrow \mathbb R^{2}$

intuitively,
1.作者认为 CTR 模型不能兼顾训练准度和校准的原因是我们有两个想要的目标, 但在默认的设定下只有一个 logit; 假如模型的输出有两个 logit, (也就是对 logit 增加一个自由度), 就能把校准和排序的目标分解开, 怎么拆开呢?
2.怎么把一个 logit 拆成 2 个? 把原本模型的输出从 1 个 logit 强行拆分成两个 logit , 一个是点击状态 logit, 一个是不点击状态 logit; 我们约定模型参数为 $\theta$ , 用 $f_{\theta}(x)[0]$ 表示非点击状态下的 logit, 且用 $f_{\theta}(x)[1]$ 表示点击状态下的 logit

$$\hat p(y|x)=\frac{1}{1+\exp(-\underbrace{(f_{\theta}(x)[1]-f_{\theta}(x)[0])}_{两个\text{logit}的差作为预估点击概率, 取代原本1个自由度下的f_{\theta}(x)})}$$

我们有了上述新的2个自由度的建模方式之后, 相应的 pointwise 的校准 loss 如下所示, 这个式子其实就是等价于两个 logits 采用了 softmax 的计算

$$\begin{aligned} \mathcal{l}_{\text{calib}}&=-\sum_{x,y}{\log}\ \hat p(y|x)\\ &=-\sum_{x,y}\log \frac{\overbrace{\exp(f_{\theta}(x)[y])}^{正样本用f_\theta(x)[1], 负样本用f_\theta(x)[0]}}{\exp(f_{\theta}(x)[1])+\exp(f_{\theta}(x)[0])} (原文用这个式子表达) \\ &=-\sum_{x,y} [\ y \cdot \log \hat p(y=1|x)-(1-y) \log (1-\hat p(y=1|x))] \ (等价于CE损失) \end{aligned}$$

3.这里我们不妨倒着想一下校准这个公式是怎么想出来的 ? 这里是要还原一下 softmax 的本质, softmax 这个函数其实就是 sigmoid 在多分类下的推广; softmax 和 sigmoid 在二分类任务上有区别吗? 完全没有, 只是有个数学上等价推导; 这里猜测作者在思考解耦 ranking 和 calibration 的时候, 还是不想放弃属于 Listwise 的建模的 naive 思想: 经典Listwise 的建模方式我们刚才提到了本质上是建模的是元素排在 Top1 的概率, 模型计算 loss 执行的是 softmax 的计算过程, 然后再这样的 softmax 和 二分类的 sigmoid 的关系中找到一种可联系二分类的的方法

$$\begin{align} output(x_1)&=\frac{1}{1+e^{-x_1}}=\text{sigmoid}(x_1) \\ &=\frac{e^{x_1}}{e^{x_1}+e^{x_2}}=\frac{1}{1+e^{-\underbrace{(x_1-x_2)}_{写成z_1}}}=\text{softmax}(x_1-x_2) \\ output(z_1)&=\frac{1}{1+e^{-z_1}}\Leftrightarrow output(x_1) \\ \end{align}$$

4.有了校准损失的解耦公式, 那么 listwise 的 ranking 损失应该怎么表达? 选择一个 session , 目标是对点击 logit 和 未点击 logit 都增加一个 listwise 的 loss 提升排序建模, 其中让正样本的点击 logit 大于 session 内其他样本的点击 logit , 让负样本的非点击 logit 大于同 session 内样本的非点击的 logit; 具体怎么做?
(i). 对于正样本, 对比的是点击logits 和其他样本的点击logits, 也就是 $f_\theta(x)[1]$
(ii). 对于负样本, 对比的是非点击logits 和其他样本的非点击logits, 也就是 $f_\theta(x)[0]$

$$l_{rank}=-\log \frac{\exp(f_\theta (x)[y])}{\sum_{x^{\prime}\in{\text{session}_x}}\exp(f_\theta({x^{\prime})}[y])} , y\in\{0,1\}$$

其实我们对比下 softmax 函数, 本质上是没有区别的

$$\text{softmax}(x)=\frac{\exp(x_i)}{\sum_{j=1}^n\exp(x_j)}$$

综合两个 loss , 得到最终的 JRC loss 如下

$$l_{\text{final}}=\alpha \mathcal l_{\text{calib}}+(1-\alpha) \mathcal l_{\text{rank}}$$

JRC pseudo code JRC代码实现

代码如下

# B: batch size, label: [B, 2], context_index: [B, 1]
# Feed forward computation to get the 2-dimensional logits 
# and compute LogLoss -log p(y|x, z)
logits = feed_forward(inputs)
ce_loss = mean(CrossEntropyLoss(logits, label))

# Mask: shape [B, B], mask[i,j]=1 indicates the i-th sample 
# and j-th sample are in the same context
mask = equal(context_index, transpose(context_index))

# 铺开 logits 和 label [B,2] => [B, B, 2]
logits = tile(expand_dims(logits, 1), [1, B, 1])
y = tile(expand_dims(label, 1), [1, B, 1])

# Set logits that are not in the same context to -inf
y = y * expand_dims(mask, 2)
logits = logits + (1-expand_dims(mask, 2))*-1e9 
y_neg, y_pos = y[:,:,0], y[:,:,1]
l_neg, l_pos = logits[:,:,0], logits[:,:,1]

# Compute listwise generative loss -log p(x|y, z)
loss_pos = -sum(y_pos * log(softmax(l_pos, axis=0)), axis=0) 
loss_neg = -sum(y_neg * log(softmax(l_neg, axis=0)), axis=0) 
ge_loss = mean((loss_pos + loss_neg) / sum(mask, axis=0))

# 合并JRC的 loss
loss = alpha * ce_loss + (1 - alpha) * ge_loss

Listwise softmax loss v.s. JRC loss

对比两种损失函数

Reference

[1]. Joint Optimization of Ranking and Calibration with Contextualized Hybrid Model.
[2]. KDD’23 | 排序和准度联合优化：一种基于混合生成/判别式建模的方案. 阿里妈妈技术. https://zhuanlan.zhihu.com/p/639569672.
[3]. KDD’23 | 阿里, 排序和校准联合建模: 让listwise模型也能用于CTR预估. 蘑菇先生. https://zhuanlan.zhihu.com/p/638414676.

---

转载请注明来源, from goldandrabbit.github.io