Overview
1.What is a Kernel? 什么是 Kernel?
2.Construct Kernels 构造 Kernel
3.Kernel Density Estimation (KDE, 核密度估计)
4.data imbalance problem: classification v.s. regression 分类和回归任务的不平衡性问题
5.challenges of imbalanced regression 不平衡回归问题面临的挑战
6.Label distribution smoothing (LDS, 标签空间的分布平滑)
7.Feature distributin smoothing (FDS, 特征空间分布平滑)
What is a Kernel? 什么是 Kernel?
Kernel is simply a function which satisfies following three properties as mentioned below.
Kernel functions are used to estimate density of random variables and as weighing function in non-parametric regression.
(i). A kernel function is that it must be symmetrical. This means the values of kernel function is same for both +u and –u as shown in the plot below. This can be mathematically expressed as $K(-u)=K(+u)$ . The symmetric property of kernel function enables the maximum value of the function $(max(K(u))$ to lie in the middle of the curve.
(ii). The area under the curve of the function must be equal to one. Mathematically, this property is expressed as $\int_{-\infty}^{+\infty}K(u)du=1$ . Gaussian density function is used as a kernel function because the area under Gaussian density curve is one and it is symmetrical too.
(iii). The value of kernel function, which is the density, can not be negative, $K(u)≥0$ for all $−∞<u <∞$.
intuitively,
1.我们核心关注针对随机变量的概率密度信息, 并且期望通过利用随机变量的概率密度信息去参与统计推断或者机器学习. Kernel 函数就是用于估计随机变量的密度的一个函数, 或者作为非参数回归中的加权函数使用; 假设我们已经有了这么一个函数, 我们只需要带入样本值, 通过 Kernel (function) 就能直接输出这个样本对应的概率密度
2.Kernel 是一个满足三个性质的函数, 所以我们谈论 kernel 的时候本质是在谈论一个 kernel function
3.为了使得这样的函数具备密度估计的功能, 沿袭概率论中的概率密度的性质 & 要达到估计密度功能, 我们对 kernel 函数的定义进行约束, 使得该函数在使用上更无缝对接密度的性质, 总结下来需要满足的三个性质分别是
(i). 对称. $K(-u)=K(+u)$ . 对称性是 kernel 的最基础的性质, 为什么一定要对称? 对称性的存在使得函数的最大值 $(max(K(u))$ 存在于曲线的正中央
(ii). 积分为1. $\int_{-\infty}^{+\infty}K(u)du=1$
(ii). 非负. $K(u)≥0$ for all $−∞<u <∞$
Construct Kernels 构造 Kernel
怎么构造 Kernel? 我们通过两阶段式的过程理解 Kernel 的构造过程
(i). 如何围绕1个样本构造 Kernel ?
(ii). 如何围绕所有的样本构造密度? 也就是如何进行Kernel Density Estimation (KDE, 核密度估计)
假设 $x_i$ 是我们观测到的数据样本, $x$ 是待计算 kernel 的变量, 也就是 Kernel 函数的输入, $K(x)$ 为 kernel 函数, $h$ 为 bandwitdh
下述演示如何围绕 1 个样本构造 kernel, 总共做两件事:
1.我们采用Gaussian kernel function 来估计 kernel density
2.(Optional) 参数估计. Kernel 函数通常是有参的形式, 我们构造 Kernel 的时候需要对函数的参数进行最优的估计; 下面的示例演示了在数据集上优化 bandwidth. 什么是 bandwidth ? 就是 Gaussian kernel function 里面的 $h$.
假设我们拿到了 6 个同学的考试分数, 我们对每 1 个样本构造一个 Gaussian kernel function.
围绕单个 $x_i$ 构造 kernel 需要三个参数
1.观测数据 $x_i$, 也就是上面的 6 个样本
2.bandwidth 参数 $h$.
3.一个能够包围观测数据范围的 lineary spaced series of data; 也就是找一个能包括数据样本的等间距数据集
# 计算 kernel 伪代码
for i in x_i:
for j in X_j:
calcu A
calcu B
K = Ae^b

然后我们将 kernel 函数可视化下, 直接 plot $X_j$ 和 $K$ , 围绕 $x_i=65$ 这个点的 kernel 如下图
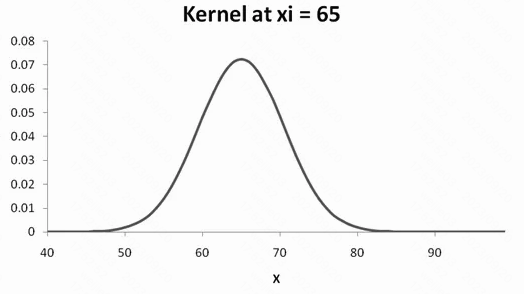
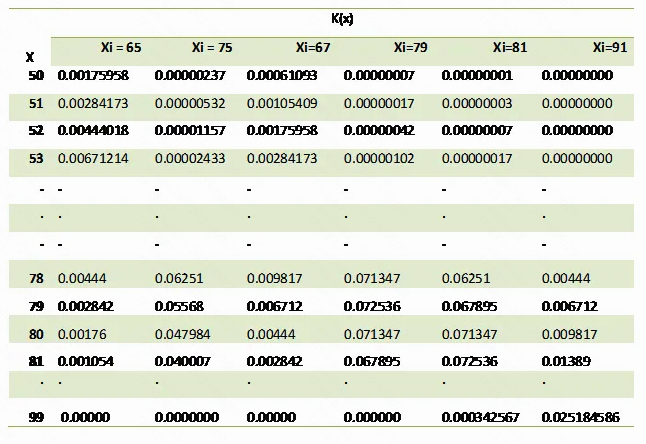
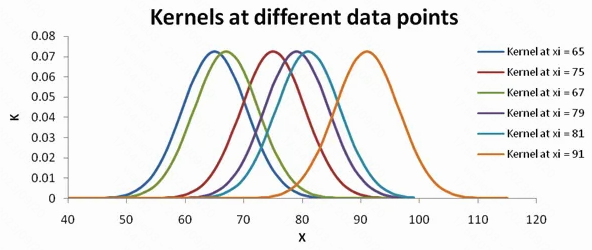
同理, 我们计算出来已有的 6 个点, 画出来所有的 kernel
Kernel Density Estimation (KDE, 核密度估计)
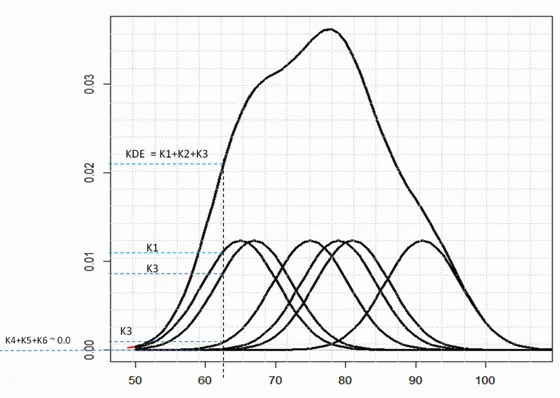
1.刚才我们说清了如何针对某个数据点构造 kernel, 那么如何针对数据集所有的数据 $x_{i}\in{65,75,67,79,81,91}$ 计算密度呢? 只需要把所有针对单独样本的 kernel 加起来, 然后再进行归一化就得到了整个数据集上的核密度估计
2.因为每个单独的 kernel 求和都是 1, 所以我们只需要在归一化操作上除以样本数, 这样得到密度估计自然满足求和等于 1
最终得到的 KDE 如下图所示
data imbalance problem: classification v.s. regression 分类和回归任务的不平衡性问题
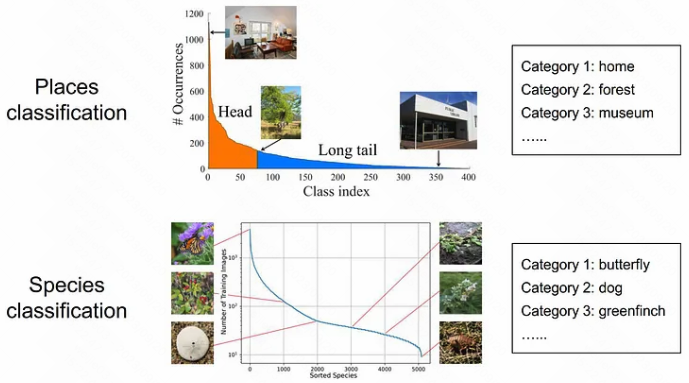
targets are categorical, and have hard boundaries with no overlapping between different classes.
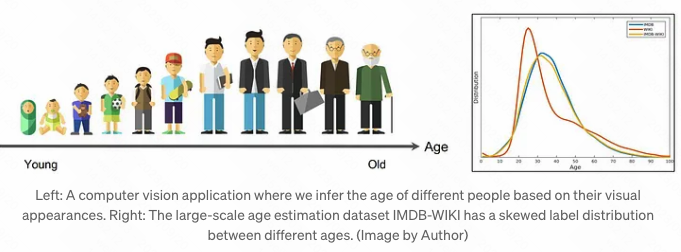
a real-world age estimation dataset, which has a skewed label distribution across different ages. In such case, treating different ages as distinct classes is unlikely to yield the best results, because it does not take advantage of the similarity between people with nearby ages.
intuitively,
1.分类问题在类目之间存在硬界限, 不同的类目之间是不存在重叠的, 例如地点分类任务中的家庭/森林/博物馆, 五中分类里面的蝴蝶/小狗/绿翅雀
2.真实世界的回归问题中, 例如年龄预测问题, (年龄的) 分布往往是有偏的; 将不同的年龄直接当做不同的类别往往效果不好, 因为没有充分利用相近的年龄之间的相关性信息
challenges of imbalanced regression 不平衡回归问题面临的挑战
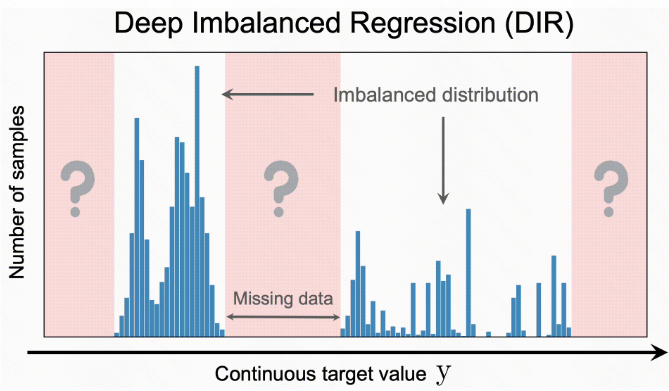
(i) given continuous and potentially infinite target values, the hard boundaries between classes no longer exist. This can cause ambiguity when directly applying traditional imbalanced classification methods such as re-sampling and re-weighting.
(ii) continuous labels inherently possess a meaningful distance between targets, which has implication for how we should interpret data imbalance in the continuous setting.
(iii) unlike classification problems, in DIR, certain target values may have no data at all, which also motivates the need for target extrapolation and interpolation.
intuitively,
1.在 ir 问题中, 硬边界不存在. 所以不能像回归问题一样, 直接采用 re-sampling 或者 re-weighting 的方法去解决 imbalanced 问题
2.连续值 label 之间存在有用的距离信息; 图中 t1 和 t2 对应的数据规模是比较小的, 但是 t1 周围临近的数据比较多, t2 周围临近的数据非常稀疏; 所以从不平衡度上看, t1 的不平衡度本质上要比 t2 要低一些
3.对于分布中某些不存在数据的 target value, 比如上图中 missing data 的位置, 需要更多地采用 value 的扩张或者插值的方式进行估计; 这里个人认为作者将这种不存在性理解成一种 bias, 所以要对 missing 进行处理, 一个好的模型不会对这些缺失”坐视不理”
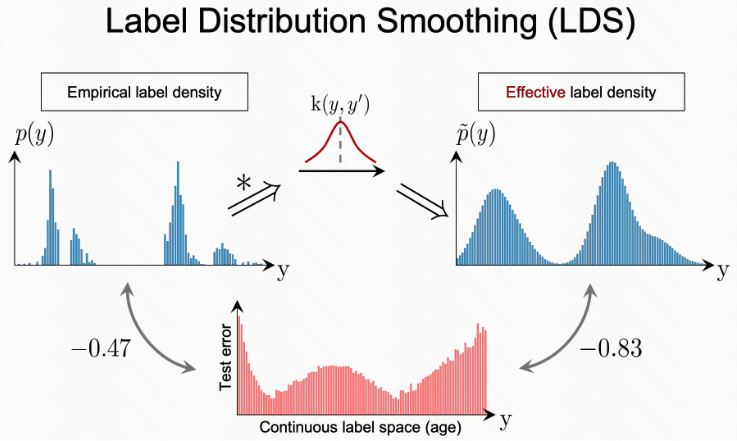
Label distribution smoothing (LDS, 标签空间的分布平滑)
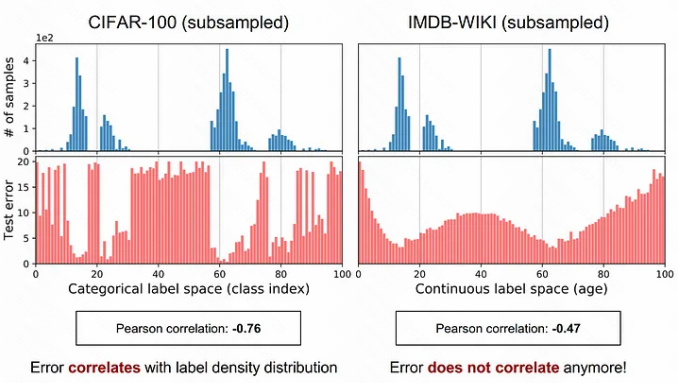
for continuous labels, the empirical label density does not accurately reflect the imbalance as seen by the model, or the neural network. Hence, in the continuous case, the empirical label distribution does not reflect the real label density distribution. This is because of the dependence between data samples at nearby labels (e.g., images of close ages).
Label Distribution Smoothing (LDS) advocates the use of kernel density estimation to learn the effective imbalance in datasets that corresponds to continuous targets.
Given a continuous empirical label density distribution, LDS convolves a symmetric kernel k with the empirical density distribution to extract a kernel-smoothed version that accounts for the overlap in information of data samples of nearby labels.
The resulting effective label density distribution, which is computed by LDS, turns out to correlate well with the error distribution now, with a Pearson correlation of −0.83
the effective label density is available, techniques for addressing class imbalance problems can be directly adapted to the DIR context. For example, a straightforward adaptation can be the cost-sensitive re-weighting method, where we reweight the loss function by multiplying it by the inverse of the LDS estimated label density for each target.
intuitively
1.这里用两个数据集去对比分类和回归在标签分布平滑上的差异:
(i). 在分类任务上, label 密度分布和 模型 error 的分布是高度相关的 (-0.74) : 数据样本少的类目上, 对应的模型误差就大; 数据样本多的类目上, 对应的模型误差就小
(ii). 在回归任务上, 连续值的经验 label 密度, 并不能反映模型学到 label 密度的分布的不平衡性 (-0.47); 也就是说在连续值预估的 case 上, 经验 label 分布不能反映真实 label 的密度分布; 这是因为相近的 label 存在一定的依赖性, 而不是像分类问题那样有硬边界
2.既然 label 的经验密度不能直接反映真实的label分布, 那应该怎么获取更真实的 label 分布信息呢?
3.采用 label 分布平滑的方式, 使用一种核密度估计的方法 (KDE) 去高效学习连续值的不平衡分布特性, 也就是 LDS
4.LDS 采用一个对称卷积核的方式 (其他核也可以?), 抽取一个 label 分布的核平滑的版本, 可以理解为一种更平滑的密度估计的方法, 能够有效提取相近的 label 之间的依赖性和重叠性信息
5.如何验证 LDS 是有效的? 也就是 LDS 给出的密度估计之后怎么验证能缓解 imbalance 的问题?
6.采用LDS给出的权重对 loss 进行加权, 对 label 设置权重为 LDS 密度的倒数, 用这样的方式发现 error 和原始的分布之间的相关性显著变好 (-0.83); 下面给出了核心 LDS reweight 的伪代码
对应的伪代码如下

7.实际使用 LDS, 核心在 loss function 上进行 reweight 操作, 我们可以对 MSE/MAE loss 中增加一行, 代码如下:
from collections import Counter
from scipy.ndimage import convolve1d
from utils import get_lds_kernel_window
# 写一个lds_kernel_window计算函数
lds_kernel_window = get_lds_kernel_window(kernel='gaussian', ks=5, sigma=2)
# 这里采用scipy可以直接支持和convolve kernel window function
eff_label_dist = convolve1d(np.array(emp_label_dist), weights=lds_kernel_window, mode='constant')
# reweight操作
from loss import weighted_mse_loss
eff_num_per_label = [eff_label_dist[bin_idx] for bin_idx in bin_index_per_label]
weights = [np.float32(1 / x) for x in eff_num_per_label]
loss = weighted_mse_loss(preds, labels, weights=weights)
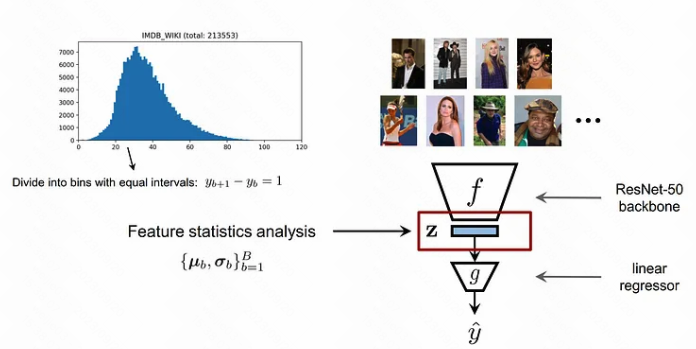
Feature distributin smoothing (FDS, 特征空间分布平滑)
motivated by the intuition that continuity in the target space should create a corresponding continuity in the feature space.
if the model works properly and the data is balanced, one expects the feature statistics corresponding to nearby targets to be close to each other.
feature statistics around the anchor bin are highly similar to their values at the anchor bin. figure confirms the intuition that when there is enough data, and for continuous targets, the feature statistics are similar to nearby bins.
intuitively,
1.连续值 label 空间我们可以实施平滑操作, 那么在对应的特征空间也可以实施相应的平滑操作; 相近 label 有依赖性, 那么相近的 label 对应的 feature 空间对应的统计特性也应该是相似的; 也就是说, FDS 目标校准特征空间中潜在的分布偏差, 在相近的连续值分桶中进行特征的统计信息迁移
2.我们用年龄预估的任务的 case 演示如何做特征空间的平滑, formulation: 特征用 $z$ 来表示, 年龄按照1作为间隔分桶, $b$ 代表分桶的编号, 计算每个分桶的特征的 mean 和 variance; 我们先选择一个桶进行研究, 这个桶称之为 anchor bin, 比如选定30岁这个桶, 记录为 $b_0$; 对比 $b_0$ 和 其他的所有的 $b$ 在特征空间的统计量 (mean & variance)
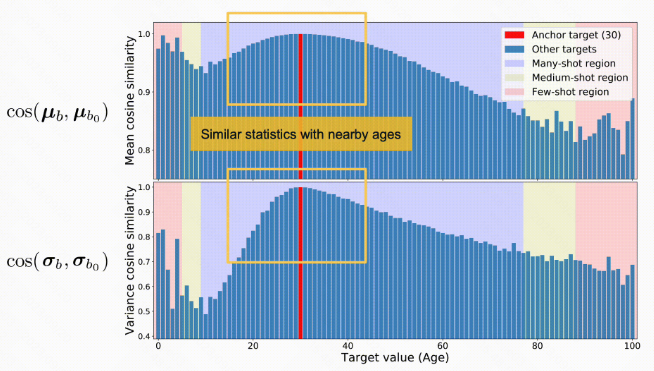
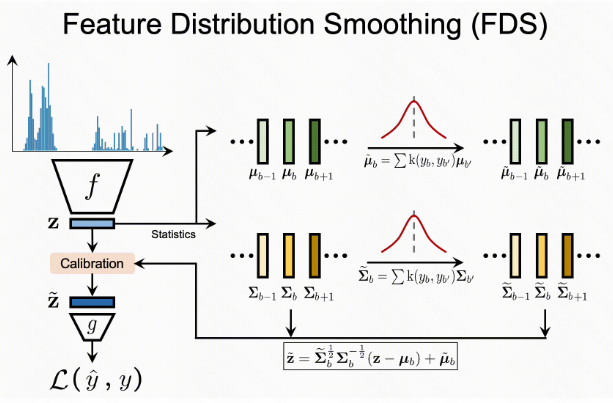
feature distribution smoothing (FDS), which performs distribution smoothing on the feature space, basically transfers the feature statistics between nearby target bins. This procedure aims to calibrate the potentially biased estimates of feature distribution, especially for underrepresented targets.
FDS is performed by first estimating the statistics of each bin. Given the feature statistics, we employ again a symmetric kernel k to smooth the distribution of the feature mean and covariance over the target bins. This results in a smoothed version of the statistics.
with both the estimated and smoothed statistics, we then follow the standard whitening and re-coloring procedure to calibrate the feature representation for each input sample. The whole pipeline of FDS is integrated into deep networks by inserting a feature calibration layer after the final feature map.
to obtain more stable and accurate estimations of the feature statistics during training, we employ a momentum update of the running statistics across each epoch.
intuitively,
1.FDS目标校准特征空间中潜在的分布偏差, 在相近的分桶中进行特征的统计信息迁移
2.首先对每个分桶计算特征的均值和协方差
3.在使用一个对称 kernel $k$ 去平滑在所有的桶上的密度, 其实就是从原有的分桶下的统计量的原始统计版本升级到了统计量的核密度版本
4.每个分桶计算出来基于核密度的均值和方差, 我们将这个操作做成神经网络的某两层: 构造一个 calibration 层 实现 whitening 再 re-coloring; 参考 Whitening and Coloring Transformations for Multivariate Gaussian Data
5.训练时候梯度下降可以用momentum更新, 能够更好地利用这些均值和方差
Reference
[1]. https://en.wikipedia.org/wiki/Kernel_density_estimation 核密度估计的介绍
[2]. https://medium.com/analytics-vidhya/kernel-density-estimation-kernel-construction-and-bandwidth-optimization-using-maximum-b1dfce127073 核密度高估计直观示例
[3]. Yuzhe Yang et al. Delving into Deep Imbalanced Regression. paper原文, 发表在 ICML 2021, 作者 from MIT
[4]. https://towardsdatascience.com/strategies-and-tactics-for-regression-on-imbalanced-data-61eeb0921fca. 作者介绍的博客.
[5]. Whitening and Coloring Transformations for Multivariate Gaussian Data. https://www.projectrhea.org/rhea/images/1/15/ Slecture_ECE662_Whitening_and_Coloring_Transforms_S14_MH.pdf
[6]. Preprocessing for deep learning: from covariance matrix to image whitening. https://hadrienj.github.io/posts/Preprocessing-for-deep-learning/
转载请注明来源 goldandrabbit.github.io