Selective-Supervised Contrastive Learning with Noisy Labels

ML_DL

Created At : 2023-06-21 20:08

Motivation
Formulation
Method
Select Confident Examples 选择置信样本
Select Confident Pair 选择置信样本对
Reference

Motivation

1.作者认为 learning with noisy label 会使得模型学到 corruppted representation, 故提出 selective-supervised contrastive learning (Sel-CL) 去解决 learning with noisy label 的问题

Formulation

$\mathcal D=\{(x_i, \tilde{y}_i)\}$ : 数据集, $x_i$是第 $i$ 个样本, $\tilde{y}_i \in [C]$ : 总共有 $C$ 个类别
$\mathcal T$ 置信样本集合/clean 样本集合

Method

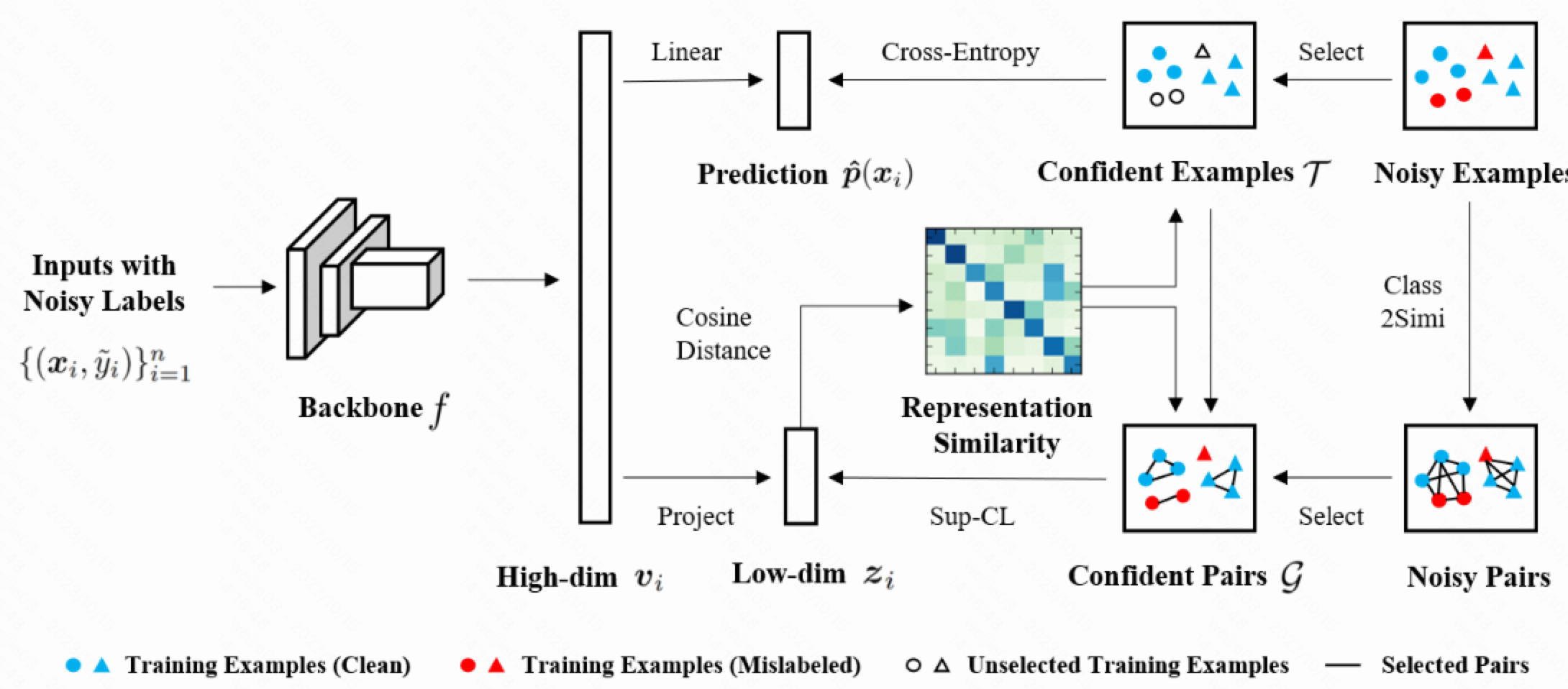
1.首先用一个 encoder $f$ 来做特征提取, 在图像输入上就是CNN backbone, 将样本 $x$ 映射到某个高维空间

Select Confident Examples 选择置信样本

1.先用 Uns-CL 进行热启训练, 训练较少的几个 epoches 得到样本的低维表达; 有了低维表达, 我们就可以利用余弦相似度得到样本间的一致性;

$d(z_i,z_j)=\frac{z_iz_j^T}{||z_i||\cdot||z_j||}$

2.对任意一个样本 $(x_i,\tilde{y}_i)$ 检索 $K$ 个相近低维表达做聚合, 得到一个 pseudo-label $\hat y_i$: 举个例子, 假设我们做的多分类问题, 且选择 $K=250$ 个最相近的低维表达中的占据主导 (占比最大的) label, 作为最终的最终的 pseudo-label $\hat y_i$

3.以上是最基础获得更 clean 的 label $\hat y_i$ 的一种方法, 实质上是利用特征空间的相似性, 采用比较 hard 的相似度检索实现样本纠偏; 除了这种方法, 我们可以继续泛化一下这种 label 纠偏的机制, 采用一种比较 soft 的方法去继续扩充 clean 样本: 首先对一个样本而言, 将 label 概率分布扩展到所有 label 类别上, 计算该样本属于所有类别的后验概率 (其实就是对所有类别求一下比例)

$\hat q_c(x_i)=\frac{1}{K}\sum_{k=1, x_k\in \mathcal N_i}^{K}\mathbb I[\hat y_k=c],c\in[C]$

我们对 $x_i$ 刚才拿到的 $\mathcal N_i$ 这么个相近的样本集合并计算出 $c$ 类别的置信度打分 $\hat q_c(x_i)$ 之后, 我们计算 cross-entropy 损失的值, 认为损失在某个较小的范围内, 该样本仍然是非常 clean 的并可以加入到 clean 样本集合: 具体来说, 对于一个样本 $x_i$ 它属于类别 $c$ 的概率, 如果 ce-loss 小于某个 (属于该类别 $c$ 的) 阈值 $\gamma_c$ 那么就认为这个样本是置信的, 就加入到置信的集合里面 $\mathcal T_c$

$\mathcal T_c=\{(x_i, \tilde{y}_i) \ | \ \text{ce-loss}(\hat q_c(x),\tilde y_i)<\gamma_c, i\in [n]\},c\in[C]$

对所有的类别 $c \in C$ 而言, 我们有了上述的方法可以得到完整的 clean data 集合

$\mathcal T=\cup_{c=1}^C\mathcal T_c$

那么这个类别阈值 $\gamma_c$ 是怎么确定的? 或者说应该如何合理地设计这个阈值？
(i). 对于每个类别 $c\in C$, 设计合理性主要应该聚焦在类别的平衡性上: 对于每个类别 $c$ 而言, 总共满足 $\alpha$ 比例的样本中 $\hat{y}_i=\tilde{y}_i$ 应该具有一致性, 写出来数量的表达式就是

$\sum_{i=1}^{n}\mathbb I\underbrace{[\hat{y}_i=\tilde{y}_i]}_{具备一致性的样本}\cdot \underbrace{[\tilde{y}_i=c]}_{挑出来c类样本}$

(ii). 比例系数 $\alpha$ 我们设定成所有类别统一的满足, 实际每个类别的参数 $\gamma_c$ 是动态变化的;

intuitively,
1.置信度样本生成的方法本质上还是利用特征空间的相似性去作为 ground truth, 然后通过检索=>聚合的方法去做 label de-noise
2.个人直觉上认为这里推广到纠偏到多分类的分布上的时候, 可以通过辅助训练一个模型去显示地刻画概率分布: 我们对 $x_i$ 刚才拿到的 $\mathcal N_i$ 这么个相近的样本集合, 训练个纠偏二分类模型 (而不是像刚才直接用后验概率做决策), 其实就是将多分类的结果转化成新建二分类任务训练, 然后通过已有的二分类模型打分出来做选择, 这样泛化性更好且直觉上可以避免后续的 $\alpha$ 参数规则带来的其他误差

Select Confident Pair 选择置信样本对

Reference

[1]. Selective-Supervised Contrastive Learning with Noisy Labels. Shikun Li et al.

转载请注明来源, from goldandrabbit.github.io