A Deep Probabilistic Model For Customer Lifetime Value Prediction

Ads_RecSys

Created At : 2023-06-13 20:43

Motivation & Challenge 主要挑战
Recap: Log-normal distribution 对数正态分布
Zero-inflate lognormal distribution (ZILN) 建模零膨胀对数正态分布
模型评估
Reference

Motivation & Challenge 主要挑战

The first is that many customers are one-time purchasers and never purchase again, resulting in many zero value labels.

The second is that for returning customers, the LTV is volatile, and the distribution of LTV is highly skewed. A few high spenders could account for a significant fraction of the total customer spend, which embodies the spirit of the 80/20 rule.

intuitively,
1.阐明了 LTV 预估模型的关键挑战:
(i). 绝大多数的 customer ltv 为 0.
(ii). 对于回头客, LTV 的波动非常大, LTV 的分布是高度有偏的且非常符合 28 定律, 非常少的客户贡献率了大多数的成交金额. 这种分布准确归类是服从 heavy-tailed 分布 (重尾分布).
2.常用的 MSE loss 在 LTV 问题上处于不可使用的状态, 在 LTV 场景上存在 2 个非常显著的缺点:
(i). 无法适应海量比例的样本 Label 0 的问题
(ii). 对头部 LTV 值极度敏感
3.提出了一个 zero-inflated lognormal (零膨胀对数正态, ZILN) 分布建模的方法, 目标建模 heavy-tailed 分布

Recap: Log-normal distribution 对数正态分布

1.Log-normal distribution (对数正态分布), 是一种连续型随机变量的概率分布, 如果一个随机变量 $x$ 符合 log-normal 分布, 意味着对 $x$ 取对数之后的随机变量 $y=\ln(x)$ 服从正态分布; 反过来推, 如果 $y$ 服从正态分布, 那么对 $y$ 取指数 $x=\exp(y)$, 服从对数正态分布
2.我们把服从对数正态分布通常记为

$\ln(x)\sim N(\mu, \sigma)$

3.对数正态分布有两个参数 $\mu\in(-\infty,\infty)$ 和 $\sigma>0$, 它的 pdf 为

$f(x)=\frac{1}{x\sigma\sqrt{2\pi}}\exp(-\frac{(\ln x-\mu)^2}{2\sigma^2})$

4.我们感受下对数正态分布的 pdf 和 cdf

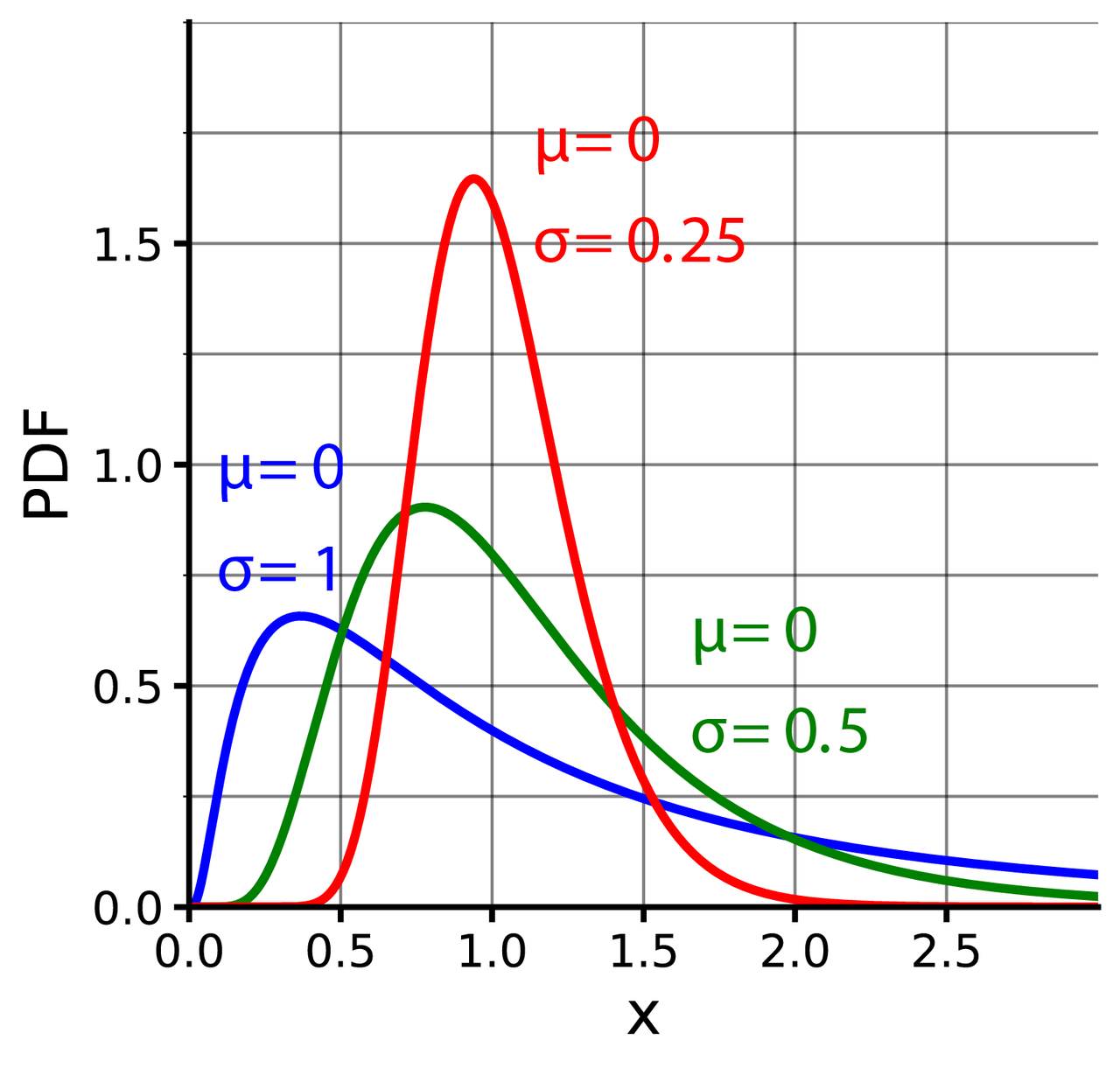
5.对数正态分布的期望和方差

$E(x)=\exp(\mu+\frac{\sigma^2}{2})\\ D(x)=(\exp(\sigma^2)-1)\exp(2\mu+\sigma^2)$

6.对数正态分布只接受 $x\in (0,\infty)$ 这种正数范围内的定义域, 很符合现实应用中正数非 0 的输入设定, 因此在很多领域都有应用

Zero-inflate lognormal distribution (ZILN) 建模零膨胀对数正态分布

建模零膨胀对数正态分布, 主要是想同时建模 [对数正态分布下的付费金额] 以及 [零膨胀的分布], 其中 [对数正态分布下的付费金额] 来自于对数正态分布的负对数似然, 如下式所示; [零膨胀的分布] 来自于单独的交叉熵损失

$\begin{aligned} \mathcal L_{\text{Lognormal}}(x;\mu,\sigma)&=-\log(\frac{1}{x\sigma\sqrt{2\pi}}\exp(-\frac{(\log x-\mu)^2}{2\sigma^2})) \\ &=\log(x\sigma\sqrt{2\pi})+\frac{(\log x-\mu)^2}{2\sigma^2} \end{aligned}$

针对 ZILN 分布, 将上面两个建模损失合并, 得到提出的新的 ZILN 损失, 其中付费金额>0 的预估概率为 $p$

$\begin{aligned} \mathcal L_{\text{ZILN}}(x;p,\mu,\sigma) &=\mathcal L_{\text{CrossEntropy}}(\mathbb I_{\{x>0\}};p)+\mathbb I_{\{x>0\}}\mathcal L_{\text{Lognormal}}(x;\mu,\sigma) \\ &=-\mathbb I_{\{x=0\}}\log(1-p)-\mathbb I_{\{x>0\}}(\log p-\mathcal L_{\text{lognormal}}(x;\mu,\sigma)) \\ &=-\mathbb I_{\{x=0\}}\log(1-p)-\mathbb I_{\{x>0\}}(\log p-\log(x\sigma\sqrt{2\pi})-\frac{(\log x-\mu)^2}{2\sigma^2}) \end{aligned}$

ZILN loss 的核心结构如下

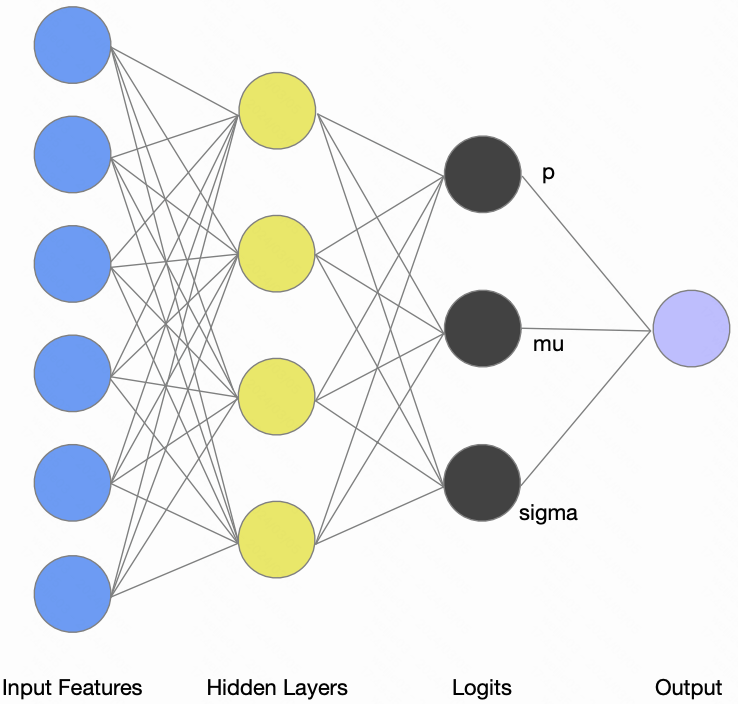
intuitively,
1.从模型结构上看, 采用的是多任务学习的方式, 有三个 logit 输出
(i). $p$: 是否付费概率, 也称为 paper 中提到的 the probabitly of returning customer
(ii). $\mu$: 对数正态分布的均值
(iii). $\sigma$: 对数正态分布的方差

2.在模型 inference 阶段, 如何计算预估出来的 ltv ? 由于对数正态分布的期望为

$E(x)=\exp(\mu+\frac{\sigma^2}{2})$

因此 inference 阶段的 ltv 预估结果为

$\text{pltv}=p\cdot \exp(\mu+\frac{\sigma^2}{2})$

模型评估

1.采用 normalized Gini coefficient (归一化基尼系数) 去量化模型辨别能力
2.采用 decile charts (十分位图) 来评估模型校准指标, 比如我们比较下如下结果

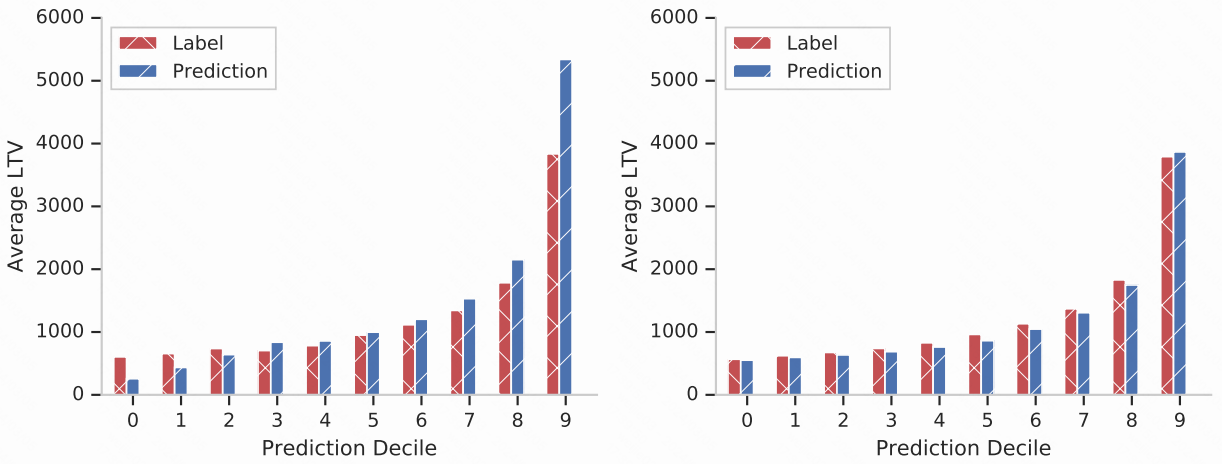
intuitively,
1.左边和右边两张图对比来看, 左边整体预估准度较差, 右边校准结果更好

Reference

[1]. Xiaojing Wang et al. A Deep Probabilistic Model For Customer Lifetime Value Prediction.
[2]. https://en.wikipedia.org/wiki/Log-normal_distribution. 介绍了正态分布的定义和性质.

转载请注明来源, from goldandrabbit.github.io