MacOS 26.1 Tahoe Upgrade

GELU: 更平滑、可微分的激活函数

GELU 高斯误差线性单元的定义是：

$$\text{GELU}(x) = x \cdot \Phi(x)$$

其中 $\Phi(x)$ 表示 标准正态分布的累积分布函数（CDF, Cumulative Distribution Function），即：

$$\Phi(x) = P(X \le x), \quad X \sim \mathcal{N}(0,1)$$

回顾 $\Phi(x)$ 数学表达式为

$$\Phi(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{x} e^{-t^2/2} , dt$$

exhuasively,

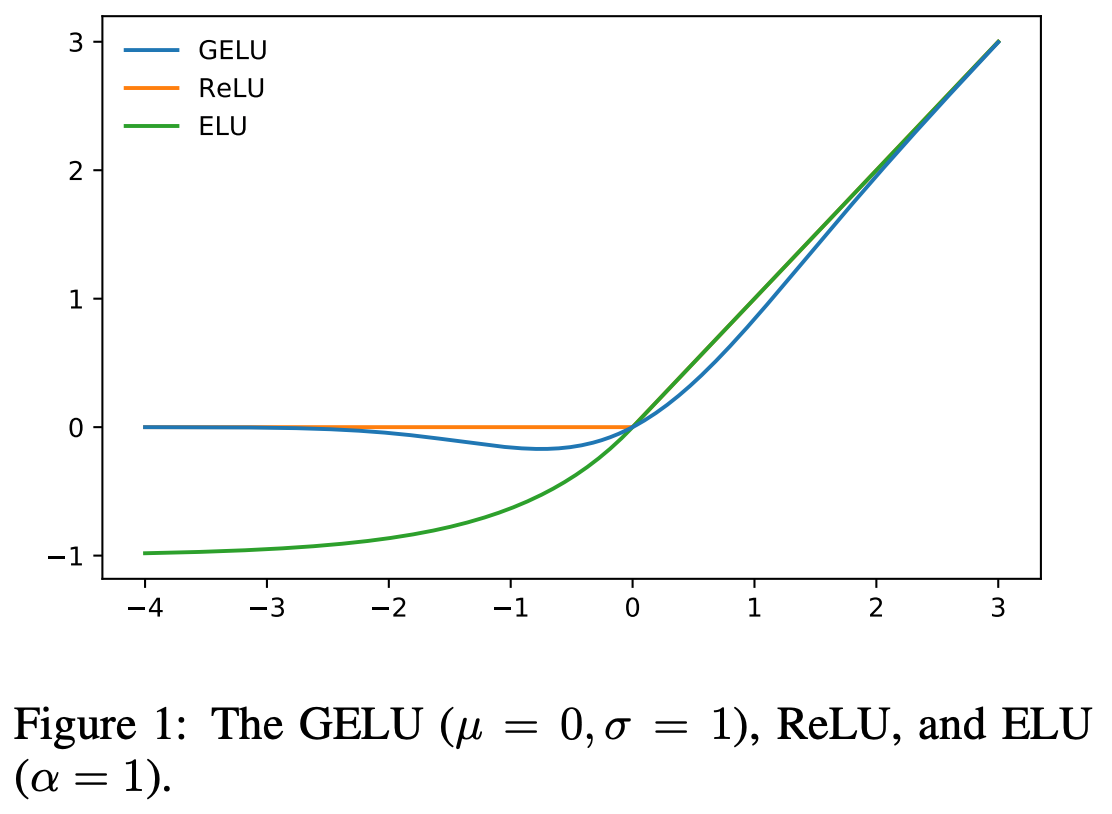
1. 它不像 ReLU 那样在 (x=0) 处有拐点（零阶可微但一阶在 0 处不连续），GELU 在整个实数域是平滑的（在理论上更” 友好” 的优化性质）
2. 平滑性带来的好处包括：梯度变化不那么剧烈、更少 “死神经元” 问题（ReLU 在负区可能完全输出 0 且梯度为 0）
3. 实际计算中, GELU 的常用近似公式为：

$$\text{GELU}(x) \approx 0.5 x \left( 1 + \tanh\Big[\sqrt{\frac{2}{\pi}} \big(x + 0.044715 x^3\big)\Big] \right)$$

1. 传统 ReLU：对负输入直接输出 0；对正输入输出 $x$; GELU 输入值” 权重化” 处理而不是简单截断：对每个输入 x，根据它 “相对于其他输入的大小” 来以概率形式决定 “激活程度” —— 用 x 与标准高斯分布（CDF）$\Phi(x)$ 相乘，从而在负区也可能有非零输出（虽然是小的）. 直觉理解：

   • 如果 x 较大，那么 $\Phi(x) \to 1$，输出接近 x.
   • 如果 x 负且很小（负很多），$\Phi(x) \to 0$，输出仍然可能比 0 略大，避免 ReLU 那样” 全部关断” 的情况.

2. 实验中显示优于一些传统激活函数: 在 Gaussian Error Linear Units 论文中，作者将 GELU 与 ReLU、ELU（Exponential Linear Unit）等函数做对比，在多个任务（计算机视觉、自然语言处理、语音）实验中都有性能提升. 社区经验中，在像 BERT、GPT‑2、GPT‑3 这样的 Transformer 架构里，GELU 也是默认使用的激活函数

3. 与正则化、优化稳定性有关的理论联系: GELU 可视为某种 “随机正则器” （类似于 dropout）期望形式的非线性函数：输入以概率方式保留或置零，这种随机化与非线性激活函数结合起来，可能有利于模型的泛化. 这种视角有助于解释为什么它在深层网络／大型模型中效果好.

Reference

[1]. Gaussian Error Linear Units.

---

转载请注明来源 goldandrabbit.github.io