Field-aware Calibration A Simple and Empirically Strong Method for Reliable Probabilistic Predictions

Ads_RecSys

Created At : 2022-08-12 20:43

Motivatin
非参数校准 v.s. 参数化校准
Platt Scaling
Isotonic Regression 保序回归
Field-ECE 指标
Neural Calibration
Isotonic Line-Plot Scaling 单调折线校准/单调分段线性放缩校准
Learning & Infer Pipeline 校准流程
Reference

Motivatin

1.提出了 field-aware 校准指标, 认为校准任务的核心考察应该是在某个 field 维度上, 例如推广计划维度, 或者游戏产品维度
2.提出了 Neural Calibration, 一种基于神经网络的残差学习校准方案

非参数校准 v.s. 参数化校准

本质区别是是否有一个映射函数

Being a parametric model (which makes assumptions about the score distributions)

Platt Scaling

1.Platt 是 1999 年提出 Platt Scaling 这种校准方法的作者; Platt Scaling 将任何一个模型的输出接入到后续一个 Logistic Regression 模型, 然后新模型输出的结果就是校准的结果; 值得注意的是, 当时提出 Platt Scaling 这种方法的动机, 待校准的模型是 SVM, SVM 的中间结果输出结果的范围是 $(-\infty, +\infty)$, 直觉上其实是缺少一个输出的概率分布校准的, 因此后续接入一个基于 Logistic Regression 的概率分布转化是非常合理的
2.对于样本 $x$ , 已有模型 $f$ 的输出为 $f(x)$

$P(y=1|f(x))=\frac{1}{1+\exp(Af(x)+B)}$

其中 $A$ 和 $B$ 是引入两个参数, 最小化的是交叉熵损失训练
3.Platt Calibration 利用了 logistic function 的输出具有输出概率的性质, 对输出结果为任意一种数据分布的情况, 尾部以 logistic function 的输出去预测为正的概率, 从而达到校准的目的; 其中参数 $A$ 和 $B$ 作为可学习的参数, 在一定程度上学习到了一种基于线性放缩的 ground truth 分布参数

Isotonic Regression 保序回归

1.保序回归, 本质是基于所有样本中某一个有序的维度, 即以一个正确的基准维度的基础上, 对另一个整体无序 (但可以理解为天然局部有序) 的维度进行校准
2.具体而言, 目标是对原有的样本 $(x,y)$ , 其中 label 是 $y$ 找到一个与它相近的 $\hat y_i$, 对所有 $x_i \le x_j$ 满足 $\hat y_i \le \hat y_j$, 也就是求解以下优化问题

$\begin{aligned} &\min\sum_{i=1}^{n}w_i(\hat y_i-y_i)^2 \\ &\text{s.t.} \ \hat y_i<\hat y_j \ \text{for all} (i,j)\in E \\ &E=\{(i,j): x_i \le x_j\} \end{aligned}$

3.保序回归是一个 hard 的校准方法, 为了严格满足某一个基准维度的有序性, 强行把另一个我们要的维度拧成有序的; 实际业务中, 如果我们确实能拿到这样的一个准确的 $x$ 维度, 那么 isonotic regression 的算法无疑是简单而强大的; 对于实时性要求很高的系统中, 我们能获得这样的一个有序的基准吗? 是很困难的, 如果我们能获得一个很强的基准, 那么我们的预估值大概率也不需要大量的校准处理了, 因为基准信号可以作为特征或者其他的因素直接建模的我们需要的预估值里面; 那为什么这个算法大概率还是有效的呢 ? 比如我们线上给出的 pctr 预估是存在显著的高估/低估问题的, 我们已有的 pctr 已经是在当前时刻给出的最优匹配效率下的预估结果, 也就是一个当前最优匹配效率下的基准信号, 在这样的信号之下如果能把准度问题处理好, 那么线上系统的可用性还是很强的
4.我们从图感受下通过保序回归过程得到的一个序列, 并对比下线性回归得到的基准

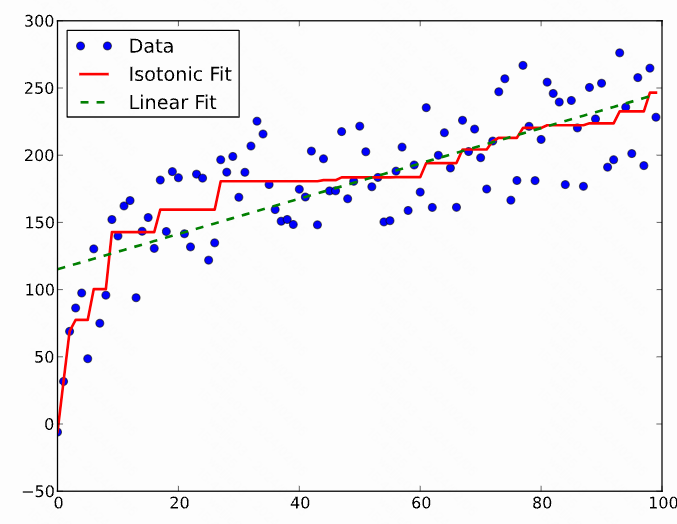
为了得到这样的 $\hat y_i$, 我们需要构造一个 non-decreasing function $f(x_i)=\hat y_i$, $f(x)$ 就是我们的校准函数

因此设计了一个专门的算法 PAV 算法: Pair Adjacent Violators (PAV) algorithm, 我把这个算法名称翻译为 [相邻逆序对区间逆转保序算法], 核心思想是遍历一遍 label, 将所有出现 [逆序对扩展出来的逆序的区间] 取平均, 直到将全部结果变成一个 [严格非降] 序列; 但这种方法通过实践我发现存在对异常点很敏感的问题, 进而衍生出来一个不能保序但是在很多场景下 work 版本: [相邻逆序对逆转局部保序算法], 核心思想是遍历一遍 label, 将所有出现 [逆序对] 取平均, 直到将全部结果变成一个 [局部非降] 序列

PAV-algo 版本 1 按照 [逆序对扩展出来的逆序的区间] 取平均, 得到的结果 [严格非降] 序列

(i). 将所有样本按照 ground truth label 排序
(ii). 迭代遍历 ground truth,
a.如果有序的话, 保序回归值等于原值, 那么往后遍历
b.如果无序的话, 记录起点, 这两个点的保序回归值更新这两个的平均, 起名为 avg; 继续往后遍历, 如果和下一个还是逆序关系, 那么继续在这 N 个平均; 直到再下一个是有序的
(iii). 处理最后一个节点

PAV-algo 版本 2 按照 [逆序对] 取平均, 无法得到 [严格保序] 序列, 得到的是 [局部非降] 序列

(i). 将所有样本按照 ground truth label 排序
(ii). 迭代遍历 ground truth,
a.如果有序的话, 保序回归值等于原值, 那么往后遍历
b.如果无序的话, 这两个点的保序回归值更新这两个的平均, 起名为 avg; 继续往后遍历, 如果和下一个还是逆序关系, 那么继续在这 2 个取平均; 直到再下一个是有序的
(iii). 处理最后一个节点

写个简单的脚本去算下

def Isotonic_Regression_v1(nums):
  res = []
  if len(nums) < 2:
    return res
  i = 0
  while (i < len(nums)-1):
    if nums[i] <= nums[i+1]:
      res.append(nums[i])
      i += 1
    elif nums[i] > nums[i+1]:
      start, end = i, i+1
      avg = sum(nums[start:end+1])/(end - start + 1)
      while end + 1 < len(nums) and avg > nums[end+1]:
        end += 1
        avg = sum(nums[start:end+1])/(end - start + 1)
      num = end - start + 1  
      res += num * [avg]
      i += num
  if i < len(nums):
    res.append(nums[-1])
  res = [round(x, 1) for x in res]
  return res

def Isotonic_Regression_v2(nums):
  res = []
  if len(nums) < 2:
    return res
  i = 0
  while (i < len(nums)-1):
    if nums[i] <= nums[i+1]:
      res.append(nums[i])
      i += 1
    elif nums[i] > nums[i+1]:
      start, end = i, i+1
      avg = sum(nums[start:end+1])/2
      res.append(avg)
      i += 1
  if i < len(nums):
    res.append(nums[-1])
  res = [round(x, 1) for x in res]
  return res

c1 = [1,2,3,4]
c2 = [1,3,2,8]
c3 = [1,3,2,2,5]
c4 = [1,10000,2,3,4,5]

print(f"nums={c1}, Isotonic_Regression_v1={Isotonic_Regression_v1(c1)}")
print(f"nums={c2}, Isotonic_Regression_v1={Isotonic_Regression_v1(c2)}")
print(f"nums={c3}, Isotonic_Regression_v1={Isotonic_Regression_v1(c3)}")
print(f"nums={c4}, Isotonic_Regression_v1={Isotonic_Regression_v1(c4)}")

print(f"nums={c1}, Isotonic_Regression_v2={Isotonic_Regression_v2(c1)}")
print(f"nums={c2}, Isotonic_Regression_v2={Isotonic_Regression_v2(c2)}")
print(f"nums={c3}, Isotonic_Regression_v2={Isotonic_Regression_v2(c3)}")
print(f"nums={c4}, Isotonic_Regression_v2={Isotonic_Regression_v2(c4)}")

输出结果

nums=[1, 2, 3, 4], Isotonic_Regression_v1=[1, 2, 3, 4]
nums=[1, 3, 2, 8], Isotonic_Regression_v1=[1, 2.5, 2.5, 8]
nums=[1, 3, 2, 2, 5], Isotonic_Regression_v1=[1, 2.3, 2.3, 2.3, 5]
nums=[1, 10000, 2, 3, 4, 5], Isotonic_Regression_v1=[1, 2002.8, 2002.8, 2002.8, 2002.8, 2002.8]

nums=[1, 2, 3, 4], Isotonic_Regression_v2=[1, 2, 3, 4]
nums=[1, 3, 2, 8], Isotonic_Regression_v2=[1, 2.5, 2, 8]
nums=[1, 3, 2, 2, 5], Isotonic_Regression_v2=[1, 2.5, 2, 2, 5]
nums=[1, 10000, 2, 3, 4, 5], Isotonic_Regression_v2=[1, 5001.0, 2, 3, 4, 5]

intuitively,
1.PAV 在很多情况下是简单有效的, 通过对局部取平均的方式, 直接把 MAE loss 快速拉下来
2.第 1 种 PAV 算法存在一个缺点, 如果存在一个非常显著的局部离群点, 取平均的过程会将部分原本不偏离太多的局部误差拉高, 例如 [1,10000,2,3,4,5] 存在一个很离谱的异常点 10000, 但是其他的, 保序回归之后得到的数字 [2002.8, 2002.8, 2002.8, 2002.8, 2002.8] 显然被平均的有点多了
3.第 2 种 PAV 不能保证是结果严格保序的, 那为什么也算做保序回归呢 ? 第二种保证了局部是有序的, 整体可能是无序的, 但是对异常值变得不敏感; 例如 [1,10000,2,3,4,5], 只对 10000 拉下来了均值, 后面的有序序列 [2,3,4,5] 的预估和真实结果完全重合而且能保序

Field-ECE 指标

for every subset of data categoried by the field $z$, the averaged prediction should agree with the averaged the field $z$.

intuitively,
1.提出 field-level 的校准指标的 motivation 很直接, 每个 field 预估均值应该应该和每个 field 的均值更相近, 所以校准指标起名为 Field Expected Calibration Error. 在 formulation 里面 $\mathcal D$ 是原始数据集, $\mathcal Z$ 是某个类目划分, 比如游戏广告对应的产品名称

$\text{Field-ECE}=\frac{1}{|\mathcal D|}\sum_{z=1}^{|\mathcal Z|}|\sum_{i=1}^{|\mathcal D|}(y_i-\hat p_i)\mathbb I_{[z_i=z]}|$

Neural Calibration

Neural Calibration 由两个部分组成协同完成校准, 延续着之前校准模型的设定, 校准操作均做在 logit 这个维度上
(i). 一个校准函数, 最简单的可以考虑保序回归的方法, 或者使用一个更强大的 Isotonic Line-Plot Scaling (ILPS) 方法
(ii). 一个神经网络, 在验证集上面去做校准训练, 用到的特征仍然是原有的特征 $x$, 实现的是 field-level 的校准
把这两个部分的输出结果加起来, 然后再通过 sigmoid 函数得到最终的输出; Neural Calibraion 的 formulation 如下

$q(l,x)=\sigma(\eta(l)+g(x))$

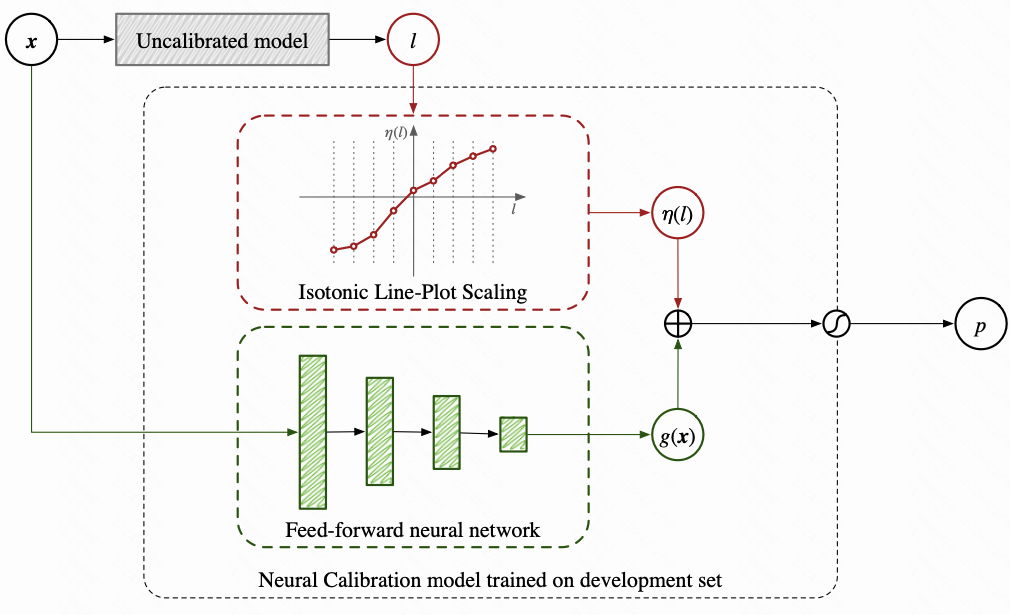
Isotonic Line-Plot Scaling 单调折线校准/单调分段线性放缩校准

如何设计更好的 $\eta(l)$ 使得满足参数化映射的要求, 同时检具单调性, 分段线性; 对值进行分桶: 预先设定好分桶上下限 $M_1$ 和 $M_2$ , 然后假设分成 $K$ 个区间

$M_1=a_1<a_2<\cdots<a_{K+1}=M_2$

然后采用以下函数计算 $\eta(l)$

$\eta(l)=b+\sum_{k=1}^{K}w_k\min\{(l-a_k)_{+},a_{k+1}-a_{k}\}$

其中,
$w_1,\ldots,w_{K}$ 和 $b$ 是可训练参数, 总参数个数是 $K+1$;
$(l-a_k)_{+}$ 是 $\max(l-a_k, 0)$ 函数的简写形式

怎么理解这个函数的设计 ? 对每一个拿到的 logit, 计算一个分段线性函数 (piece-wise linear funcion) 的输出, 拆开来看这个式子可以分成三种情况,

$\eta(l)=\left\{\begin{matrix} &w_{k}(a_{k+1}-a_{k})+b \quad \text{for} \ a_{k+1}<l \\ &w_{k}(l-a_{k})+b \quad \text{for} \ a_k <l <a_{k+1} \\ &b \quad \text{for} \ a_k>l \end{matrix}\right.$

采用分段线性函数做参数化的 scaling, 画出来的图像类似于折线图, 因此将这种参数化的校准方式命名为 Isotonic Line-Plot Scaling, 我们内心明白本质上用的是分段线性函数这种映射方式; 在此基础上提出了一个改进版, 可以显著降低训练过程中的参数量; 我们发现训练过程中, 对于样本 $l$, 都用到了 $l$ 之前所有的 $w_k$ 参数, 再加上当前区间的参数, 总共 $k+1$ 个参数; 这里我们可以对这个形式进行一定的优化, 使得任意一个样本只用两个端点参数, 也就是缩小到 2 个参数

$\eta(l)=\sum_{k=1}^{K}[b_k+(l-a_k)\frac{b_{k+1}-b_{k}}{a_{k+1}-a_k}]\mathbb I_{[a_k,a_{k+1}]}(l)$

其中,
$b_k$ 是第 $k$ 个区间左侧端点的 bias 项
$\frac{b_{k+1}-b_{k}}{a_{k+1}-a_k}$ 是第 k 个区间的斜率
在上式的设定下, 在第 $k$ 个区间的样本的参数化的校准映射只需要用两个参数 $b_k$ 和 $b_{k+1}$ 去控制, 最终的待学习参数可表示为为一个长度为 $K+1$ 的向量 $b=(b_1,\ldots,b_{K+1})$, 总参数量仍然是 $K+1$ 个待训练参数, 没有任何参数增加;
有了上述形式化的设计, 并不能保证 isotonic 的性质, 我们期望在上述的学到的 $b_k$ 上面增加一些约束, 使得 $b_k$ 满足单调性, 思路上是实现拉格朗日方法: 通过在损失函数上增加一些正则项去约束单调性, 因此我们得到完整的 ILPS 方法的损失函数如下

$\mathcal L_{\text{ILPS}}=\text{LogLoss}(\eta(l),y)+\lambda\sum_{k=1}^{K}(b_k-b_{k+1})_{+}$

intuitively,
1.对任何区间不具备单调性的 $b_k$ 和 $b_{k+1}$ 进行惩罚
2.实际使用中, 取 $K=100$ 这种分桶设定

Learning & Infer Pipeline 校准流程

step1.将数据集分为 $\mathcal D_{train}$ 和 $\mathcal D_{dev}$
step2.在 $\mathcal D_{train}$ 上训练 base 模型 $f$
step3.在 $\mathcal D_{dev}$ 上训练 Neural Calibration 校准模型 $q(l,x)=\sigma(\eta(l)+g(x))$
step4.inference 两步走: 先在未校准的 base 模型上输出 $l=f(x)$, 然后通过校准模型输出 $\hat p=q(l,x)=\sigma(\eta(l)+g(x))$

Reference

[1]. https://en.wikipedia.org/wiki/Platt_scaling.
[2]. Predicting Good Probabilities With Supervised Learning.
[3]. Field-aware Calibration: A Simple and Empirically Strong Method for Reliable [Probabilistic Predictions.
[4]. https://www.abzu.ai/data-science/calibration-introduction-part-2/.
[5]. Transforming Classifier Scores into Accurate Multiclass Probability Estimates.
[6]. 模型校准 calibration. https://zhuanlan.zhihu.com/p/101766505.

转载请注明来源, from goldandrabbit.github.io