Mechanism Design 机制设计_1_Learning-based Mechanism

Ads_RecSys

Created At : 2022-03-12 23:00

Overview
Auction Design Basics
Reference

Overview

1.RegretNet: Optimal Auction through Deep Learning 遗憾网络: 通深度学习下的最优拍卖
2.Neural Auction: End2End Auction 端到端的多目标机制学习
3.Context-Intergrated Auction 考虑上下问的拍卖机制

Auction Design Basics

通过 Deep Learning 的方法优化 Mechanism Design, 其中 Auction Design 定义如下

A set of $n$ bidders $N=\left {1,…,n \right }$ and $m$ items $M=\left {1,…,m \right }$.Each bidder $i$ has a valuation function $vi: 2^M \to \mathbb R{\ge 0}$, where $v_i(S)$ denotes how much the bidder values the subset of items $S \subseteq M$.

If a bidder may have additive valuations. In this case she has a value $vi (\left {j \right })$ for each individual item $j\subseteq M$, and her value for a subset of items $S \subseteq M$ is $v_i(S) = \sum{j\in S}vi(\left {j \right })$.If a bidder’s value for a subset of items $S \subseteq M$ is $v_i(S)={\rm max}{j\in S} v_i(\left {j \right })$, we say this bidder has a unit-demand valuation. We also consider bidders with general combinatorial valuations.

Bidder $i$ ‘s valuation function is drawn independently from a distribution $Fi$ over possible valuation functions $V_i$. We write $v = (v_1,…,v_n)$ for a profile of valuations, and denote $V=\prod{i=1}^{n} V_i$. The auctioneer knows the distributions $F = (F_1,…,F_n)$, but does not know the bidders’ realized valuation $v$. The bidders report their valuations (perhaps untruthfully), and an auction decides on an allocation of items to the bidders and charges a payment to them.

We denote an auction

$(g, p)$

as a pair of allocation rules $gi: V \to 2^M$ and payment rules $p_i: V \to \mathbb R{\ge 0}$ (these rules can be randomized).Given bids $b = (b_1,…,b_n) \in V$ , the auction computes an allocation $g(b)$ and payments $p(b)$.

A bidder with valuation $v_i$ receives a utility

$u_i(v_i; b) = v_i(g_i(b)) − p_i(b)$

for a report of bid profile $b$. Let $v{−i}$ denote the valuation profile $v=(v_1,…,v_n)$ without element $v_i$, similarly for $b_i$, and let $V_i=\prod{j\ne i} V_j$ denote the possible valuation profiles of bidders other than bidder $i$.

1.An auction is dominant strategy incentive compatible (DSIC) if each bidder’s utility is maximized by reporting truthfully no matter what the other bidders report. In other words,

$u_i(v_i; (v_i; b_{−i})) \ge u_i(v_i; (b_i; b_{−i}))$

for every bidder $i$, every valuation $vi \in V_i$, every bid $b_i \in V_i$, and all bids $b{−i} \in V_{−i}$ from others.

2.An auction is ex post individually rational (IR) if each bidder receives a non-zero utility, i.e.

$u_i(v_i; (v_i; b_{−i})) \ge 0$

for $\forall i \in N, vi \in V_i$, and $b{−i} \in V_{−i}$.

In a DSIC auction, it is in the best interest of each bidder to report truthfully, and so the revenue on valuation profile $v$ is

${\textstyle \sum_{i} {p_i(v)}}$

Optimal auction design seeks to identify a DSIC auction that maximizes expected revenue.

Formulation as a Learning Problem

given a parametric class of auctions $(g^w, p^w) \in \mathcal M$, for parameter $w \in \mathbb R^d$ for some $d \in \mathbb N$, and sample a bidder valuation profiles $\mathcal S=\left {v^{(1)},…,v^{(L)} \right }$ drawn i.i.d from $F$. The goal is to find an auction that minimizes the negated, expected revenue

$-\textbf E \left [{\textstyle \sum_{i \in N}} p_i^w(v) \right]$

RegretNet

RegretNet replace IC constraints with a differenctiable approximation and lifts the IC constraints into the objective by augmenting the objective with a term that account for the extent to which the IC constraints are vialated.

RegretNet measure the extent to which an auction violates the incentive compatibility through the following notion of ex post regret.

Fixing the bids of others, the ex post regret for a bidder is the maximum increase in her utility, considering all possible non-truthful bids. For mechanisms $(g^w, p^w)$, RegretNet is interested in expected ex post regret for bidder $i$：

$rgt_i(w)= \textbf E \left[\mathop{\rm max}\limits_{v'\in V_i} u_i^w(v_i;(v_i^{\prime},v_{-i}))-u_i^w(v_i;(v_i,v_{-i})) \right]$

where the expectation is over $v \sim F$, and $u_i^w(v_i;b)=v_i(g_i^w(b))-p_i^w(b)$ for model parameters $w$

Neural Auction

传统拍卖机制的局限
(i). 单一目标优化：传统 GSP/VCG 等机制仅关注收入或社会福利等单一目标, 难以平衡广告主、平台和用户的多方利益
(ii). 静态分配规则：基于线性组合的排序策略 (如uGSP) 依赖预估模型的准确性, 无法动态调整流量波动和预估偏差
(iii). 广告主模型失配：传统机制假设广告主为”效用最大化”(utility-maximizer), 但实际场景中存在 OCPC、MCB 等新型广告主类型, 其行为更符合 “价值最大化” (value maximizer) 模型

intuitively,
论文首次将广告主行为模型拓展为 Value Maximizer, 并通过以下约束保障机制的经济学性质
(i). 单调分配(Monotonicity)：广告主提高报价不会获得更差的分配
(ii). 最小扣费(Critical Price)：胜出广告按获得相同坑位的最低报价计费

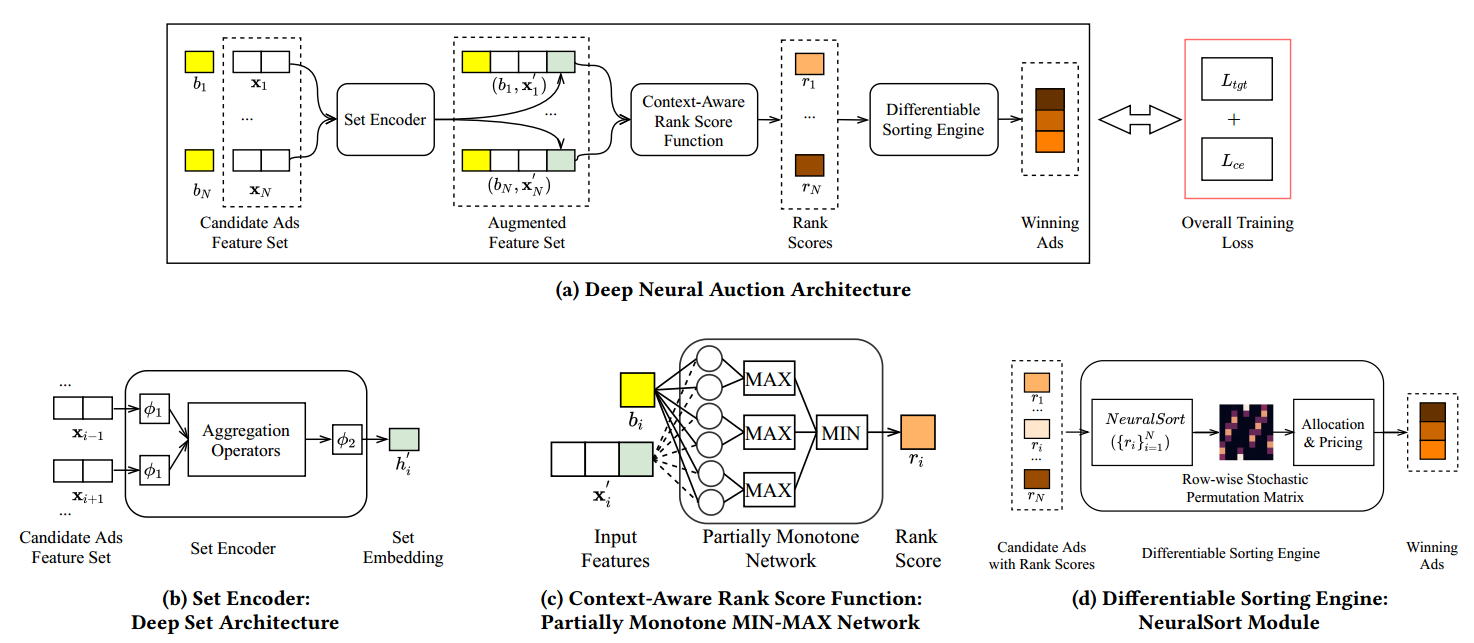
DNA 框架通过端到端学习和可微分算子实现了拍卖机制的动态优化, 其核心模块包括：
1.集合编码器 (Set Encoder)
使用 DeepSet 网络建模广告候选集的上下文信息, 通过共享编码器提取特征后聚合, 保持排列不变性 (permutation invariance)

2.上下文评分函数 (Context-Aware Rank Score Function)
设计部分单调最小最大网络(Partially Monotone Min-Max Network), 确保评分函数在出价维度上的单调性, 满足IC/IR约束

3.可微排序引擎 (Differentiable Sorting Engine)
引入 NeuralSort 技术, 通过 softmax 松弛离散排序过程, 构建可微分的置换矩阵, 实现排序结果与反馈信号的梯度回传

Reference

[1]. Optimal Auctions through Deep Learning. Paul Dütting et al.
[2]. Neural Auction: End-to-End Learning of Auction Mechanisms for E-Commerce Advertising https://arxiv.org/abs/2106.03593. Xiangyu Liu et al.
[3]. Neural Auction: 电商广告中的端到端机制优化方法 https://zhuanlan.zhihu.com/p/412872425. Xiangyu Liu et al.

转载请注明来源 goldandrabbit.github.io