
Overview
1.What is Mechanism Design? 什么是机制设计
2.Mechanism Design Basics 机制设计中的基础概念
3.Auction Basics 拍卖中的基础概念
4.Idea Auctions 理想的拍卖机制
5.Myerson’s Lemma 迈尔森引理
6.Vickrey-Clarke-Groves Mechanisms VCG 机制
What is Mechanism Design? 什么是机制设计
Mechanism design can be viewed as the reverse engineering of games or equivalently as the art of designing the rules of a game to achieve a specific desired outcome.
The main focus of mechanism design is to create institutions or protocols that satisfy certain desired objectives, assuming that the individual agents, interacting through the institution, will act strategically and may hold private information that is relevant to the decision at hand.
intuitively,
1.机制设计是博弈的逆向工程. 假如此时我们在和对面 (可能有多家) 玩游戏比谁得分高/杀掉对方为获胜等等, 我们在发生博弈; 但是这些”游戏”都有一个设计规则的人, 这个设计游戏规则的人有上帝视角权限很大, 这个设计游戏规则的人干的事情就是机制设计
2.对于任何博弈/游戏来说, 通过理想的机制设计, 有可能使得大家在博弈的过程中实现共赢的局面, (注意只是有可能实现, 有些博弈的类型决定了没办法共赢), 如果实现了能够让大家共赢的局面, 那就相当优雅了, 因此说是设计规则以实现特定结果的艺术
3.我们再精确的定义下机制设计是在做什么 ? 创造满足一定合意目标的制度或者规则, 以引导在制度中互动的智能体 (参与人) 实施策略性行动, 并能保留与决策相关的私人信息
Mechanism Desgin Basics 机制设计中的基础概念
There are $n$ agents with $N={1,2,..,n}$. The agents are rational and intelligent, and interact strategically among themselves towards making a collective decision.
$X$ is a set of alternatives or outcomes. The agents are required to make a collective choice from the set $X$.
Prior to making the collective choice, each agent privately observes his preferences over the alternatives in $X$. This is modeled by supposing that agent $i$ privately observes a parameter or signal $\theta_i$ that determines his preferences. The value of $\theta_i$ is known to agent $i$ and may not be known to the other agents. $\theta_i$ is called a private value or type of agent $i$.
We denote by $Θ_i$ the set of private values of agent $i$, The set of all type profiles is given by $\Theta=\Theta_1 \times , … , \times \Theta_n$. A typical type profile is represented as $\theta=(\theta_1,…,\theta_n)$.
We assume that there is a common prior $\mathbb{P} \in \Delta (\Theta)$. To ensure consistency of beliefs, individual belief functions $pi : \Theta_i \to \Delta (\Theta{−i})$ (where $\Theta_{−i}$ is the set of type profiles of agents other than $i$) can all be derived from the common prior.
Individual agents have preferences over outcomes that are represented by a utility function $ui : X \times \Theta{i} \to \mathbb{R}$. Given $x \in X$ and $\theta_i \in Θ_i$, the value $u_i(x, \theta_i)$ denotes the payoff that agent $i$, having type $\theta_i \in \Theta_i$, receives from an outcome $x \in X$. In the more general case, $u_i$ depends not only on the outcome and the type of player $i$, but could depend on the types of the other players as well, and so $u_i: X \times \Theta \to R$.
The set of outcomes $X$, the set of players $N$, the type sets $\Theta_i$, the common prior distribution $\mathbb{P} \in \Delta (\Theta)$, and the payoff functions $u_i$ are assumed to be common knowledge among all the players. The specific type $θ_i$ observed by agent $i$ is private information of agent $i$.
intuitively,
1.上面机制设计概念的定义是数学化的定义非常系统但是其实都是源自于生活的博弈抽象, 理解上我们需要建立一些基础的直觉, 并通过一些例子去理解, 最经典的就是拍卖的例子
2.总共有 $N$ 个智能体 (想象成几个人类也可以, 只不过和日常生活中的人相比过于冷血无情) 参与博弈, 比如参加拍卖. 参与拍卖的智能体有两个非常关键的属性 rational 和 intelligent, 这两个假设是非常基础且重要的, 我们逐个理解下
(i). rational:
(ii). intelligent:
3.任何博弈或者游戏最终都会有个结果, 这就是 alternatives 或者称为 outcomes. 比如在一轮拍卖中出价最高的人得到物品, 其他人什么也没有得到 (当然也什么也没有失去), 这种结果可以编码成非 1 即 0 的二分类空间. 另外有时候结果可能是多种的, 比如 5 个人每个人各自玩一局 Atari, 按照分数就可以搞个排名.
4.对于每个人来说, 都有属于自己的一套 type profile 或者称为 private value, 可以理解为智能体的决策框架, 或者说按照怎么样的策略来进行动作, 比如人类大脑的思考逻辑, 或者决策神经网络的参数. 每个人的一套参数里面可能有多种策略, 每次博弈用自己的哪一套策略不一定. 比如玩 war3 游戏 1v1 我第一把可以非常激进地一本爆兵 tower rush 不给对手喘息的机会, 第二把可以非常猥琐地开分矿然后造塔稳住经济在拼后期, 第三把可以打个常规套路稳扎稳打拼操作. 有些时候博弈的多方都有自己的一套参数集合. 所有参与人的所有策略构成了一个可能巨大的向量空间. 同时, 这个私人的参数通常具备私人性, 每个人都有自己的一套理解和策略, 因此是个 private information.
5.对于每个人来说, 对于自己在某种决策下的某种结果, 都有个评价, 这就是 preference. 比如初中一次期末考试, 大家比的是考试结果的总分排名. 比如 A 是个普通学生好好学习了, 班级排名第 15 觉得挺好了. 有个学渣同学基础比较薄弱且没有怎么复习 (姑且认为是能力不足而不是主观意愿上的不爱比成绩) 考了个 50 名觉得也挺好. C 是稳定的学霸, 之前每次都是第 1, 这次是第 2, 感觉人生都迷茫了无法接受. 可见每个人在博弈过后对结果上都是有一些评价的, 这个评价可以写成一个 utility function 效用函数, 函数的输入是和自己的代价和结果, 输出是对这个结果的评价, 这个评价可以定义成一个实数.
Auction Basics 拍卖中的基础概念
1.拍卖是一种典型的博弈, 参与竞拍的人就是博弈的参与者, 拍卖有报价+结果两个环节构成
2.拍卖的机制设计是一类经典的问题, 我们理解机制设计不妨从拍卖入手去理解上述机制设计的核心概念
Sealed-Bid Auctions 密封拍卖
1.Each bidder $i$ privately communicates a bid $b_i$ to the seller-in a sealed envelope.
2.The seller decides who gets the item.
3.The seller decides on a selling price.
intuitively,
1.所谓密封拍卖, 就是每个人都是悄悄报价, 只有自己知道自己的报价, 别人不知道自己的报价, 自己也不知道别人的报价. 早期互联网广告竞价就是一种典型的密封拍卖, 广告主在系统上充钱之后, 填写自己报价.
2.卖家决定了谁最终决定谁得到最终的物品, 以及以什么价格支付这个物品.
Sencod-Price Auction (Vickrey Auction) 二价拍卖 (维克里拍卖)
Incentives in Second-Price Auctions. In a second-price auction, every bidder $i$ has a dominant strategy: set the bid $b_i$ equal to her private valuation $v_i$.
Proof: Incentives in Second-Price Auctions 二价拍卖中的激励兼容性的证明
Fix an arbitrary bidder $i$, valuation $vi$, and the bids $b{-i}$ from other bidders. We need proof that bidder $i$’s utility is maximized by setting $bi=v_i$. Let $B=\max{j\ne{i}} b_j$ denotes the highest bid by some other bidder. What’s special about a second-price aucton is that, even though distinct outcomes can result.
If $b_i < B$, then $i$ loses and receives utility 0.
If $b_i \ge B$, then $i$ wins at $B$ and receives utility. $v_i - B$
We conclude by considering two cases.
First, if $vi < B$, the maximum utility that bidder $i$ can obtain is max $\left{ 0, v{i}-B \right }=0$, and it achieves that by bidding truthfully (and losing).
Second, if $v_i \ge B$, the maximum utility that bidder $i$ can obtain is max $\left{0, v_i - B \right}=v_i - B$.
Nonnegative Utility. In a second-price auction, every truthful bidder is guranteed nonnagative utility. In other words, one that bids her true valuation-never regrets participating in the second-price auction.
Proof: Nonnegative Utility
Losers receive utility 0. If a bidder $i$ is the winner, then her utiliy is $v_i - p$, where $p$ is the second-highest bid. Since $i$ is the winner (and hence the highest bidder) and bid her true valuation, $p \le v_i$ an hence $v_i - p \ge 0$.
Ideal Auctions 理想的拍卖机制
Dominant-Strategy Incentive Compatible 占优策略激励兼容
An auction is dominant-strategy incentive compatible(DSIC) if truthful bidding is always a dominant for every bidder and if truthful bidders always obtain nonnegative utility.
优势策略激励兼容: 对每个bidder来说, 讲真话是优势策略且总是非负效用.
Define the socal welfare of an outcome of a singe-item auction by
where $xi$ is 1 if $i$ wins and $0$ if i loses. Because there is only on item, we have the feasibility constraint that $\sum\nolimits{i=1}^{n}x_i \le 1$. Thus, the social welfare is just the valuation of the winner, or 0 if there is no winner. An auction is is welfare maximizing if, when bids are truthful, the auction outcome has the maximum possible social welfare.
Three properties of Ideal Auctions
A second-price single-item auction satisfies the following:
1.[strong incentive guarantees] It is a DSIC auction.
2.[strong performance guarantees] It is welfare maximizing.
3.[computational efficiency] It can implemented in time poly-nomial(indeed, linear) in the size of the input, meaning the number of bits necessary to represent the numbers $v_1,…,v_n$
Why three properties are important?
1.DSIC.
From a bidder’s perspective, the DISC property makes it particularly easy to choose a bid, and levels the playing field between sophisticated and unsophischated bidders;
From the perspective of the seller or auction designer, the DSIC property makes it much easier to reason about the auction’s outcome. Note that any prediction of an auction’s outcome has to be predicted on assumptions about how bidders behave. In a DSIC auction, the only assumption is that a bidder with an obvious dominant strategy will pay it.
2.Welfare maximization property.
This property states something rather amazing: even though the bidder valuations are a priori unknown to the seller, the auction nevertheless identifies the bidder with hightest valuation. That is, a second-price auction solves the social welfare maximization problem as well as if all of the bidders’ valuations were known in advance.
3.Computational efficiency.
An auction should run in a reasonable amount of time. For example, auctions for online advertising.
Myerson’s Lemma 迈尔森引理
Allocation and Payment Rules 分配和支付规则
Sealed-bid auction has to make two choices: who wins and who pays what. These two decisions are formalized via an allocation rule and a payment rule, respectively. Here are the three steps:
1.Collect bids $\bf b=(b_1,…,b_n)$ from all agents. The vector $\bf b$ is called the bid vector or bid profile.
2.[allocation rule] Choose a feasible allocation $\bf{x(b)} \in X \subseteq \mathbb R^{n}$ as a function of the bids.
3.[payment rule] Choose payments $\bf{p(b)} \in \mathbb R^n$ as a function of the bids.
Procedures of this type are called direct-revelation mechanisms, because in the first step agents are asked to reveal directly their private valuatons.
这种机制叫直接显示机制.
With our quasilinear utility model, in a mechanism with allocation and payment rules $x$ and $p$, respectively, agent $i$ receive utiliy:
when the bid profile is $\bf b$.
We focus on payment rules that satisfy
for every agent $i$ and bid profile $\bf b$.
The constraint that $p_i(\bf b) \ge 0$ is equivalent to prohibiting the seller from paying the agents.
The constraint that $p_i(\bf b) \le b_i \cdot x_i(\bf b)$ ensures that a truthful agents receives nonnegative utility.
Allocation Rule: Implementable and Monotone 分配规则: 可实施和单调性
Implementable. An allocaton rule $\bf x$ is single-parameter enviroment is implementable if there is a payment rule $\bf p$ such that direct-revelation mechanism $\bf{(x, p)}$ is DISC.
Monotone An allocation rule $\bf x$ for a single-pamameter enviroment is monotone if for every agent $i$ and bids $b{-i}$ by the other agents, the allocation $x_i(z, b{-i})$ to $i$ is nondecreasing in her bid $z$.
Myerson’s Lemma 迈尔森引理的具体内容
Fix a single-parameter enviroment,
(a) An allocation rule $\bf x$ is implementable if and only if it is monotone.
分配规则中的可实施性和单调性是等价的.
(b) If $\bf x$ is monotone, then there is a unique payment rule for which the direct-revelation machanism $\bf{(x, p)}$ is DSIC and $p_i(\bf b)=0$, whenever $b_i=0$.
如果分配规则是单调的, 那么存在唯一的支付规则使得机制是DISC的.
(c) The payment rule in (b) is given by an explicit formula.
(b)中的支付规则有明确的表达式.
Myerson’s lemma is the foundation on which we’ll build most of our mechanism design theory.
迈尔森引理是大多数机制设计理论的基石.
Part(a) states that implementable and momotone are exactly the same class, implementable is unwiedly to work with and verify, but Monotone is more operational. Monotone is easy to check.
第一部分告诉我们分配的可实施性和单调性是等价的, 但是 [可实施性] 的概念是模糊不清的, 是辨别的. 但是单调性是非常容易辨别的.
Part(b) states that when an allocation rule is implementable-there is only way to assgin payment rule.
第二部分告诉我们可实施的分配规则只有唯一的支付规则.
Part(c) states there is a relatively simple and expicit formula for payment rule.
第三部分告诉我们有一明确的支付规则解析式.
Payment rule of Myerson’s Lemma 迈尔森引理的支付规则
Fix $i$ and $\bf b{-i}$ arbitrarily, write $x(z)$ and $p(z)$ for allocation $x_i(z, b{-i})$ and payment $pi(z, \bf b{-i})$ of $i$ when she bids $z$.
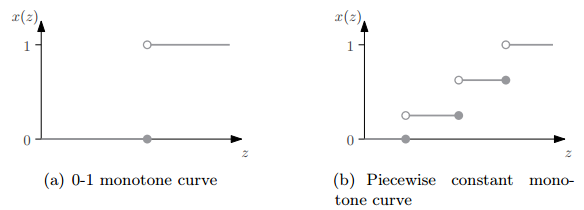
consider the case where $x$ is piecewise constant function as above Fig. The graph of $x$ flat except for a finite number of “jumps”. If there is a jump of magnitude $h$ at $z$, then left- and right-hand sides both tend to $z \cdot h$, this implies the following constraint on $p$, for every $z$:
combining this with the initial condition $p(0)=0$, we’ve derived the payment formula, for every agent $i$, bids $\bf b_{-i}$ by other agents, and bid $b_i$ by $i$:
where $z1,…,z_l$ are the breakpoints of allocation function $x_i(\cdot, \bf b{-i})$ in the range $[0, b_i]$.
Vickrey-Clarke-Groves Mechanisms VCG 机制
General Mechanism Design Enviroments
In single-parameter mechanism design, only private parameter of an agent is her valuation per unit of stuff, for multi-pamameter-problems, each agent has multiple private parameters.
A general multi-parameter mechanism design enviroment comprises following ingredients:
1.n asttegric agents;
2.a finite set $\Omega$;
3.each agent $i$ has a private nonnegative evaluation $vi(\omega)$ for each outcome $\omega \in \Omega$;
The outcome set $\Omega$ is abstract and could be very large. The social welfare of an outcome $\omega \in \Omega$ is defined as $\sum\nolimits{i=1}^{n}v_i(\omega)$.
Example1: Single-Item multi-parameter pamameter
In a bidder war over a hot asttup, if a bidder loses, she might prefer that the asttup be bought by a company in a different market, rather than by a direct competitor.
intuitively,
在对一个热门公司的竞购战中, 如果一个竞拍者输了他更希望来自于其他市场收购这家公司, 而不是被自己的直接竞争者收购.
我想到一个类似例子: 曼城、曼联和皇马都想要姆巴佩, 如果曼联铁定拿不到, 它更希望皇马得到而不是同联赛对手曼城拿到, 一种可能的情形皇马8.0, 曼城 7.9, 曼联 6.0, 若皇马出价意愿略高于曼城, 这时候曼联可以调整出价到 9.0, 皇马可以出价到 9.1, 但曼城可能最高 8.5, 这时候皇马得到且曼城失败, 实施这种出价策略扩大了皇马和曼城之间的出价差距; 因此在一场拍卖博弈中对于同一标的采用不同的估值策略
Example2: Combinatorial Auction
There are multiple dindivisible items for sale, and bidders can have complex preference between different subsets of items(called buddles). With $n$ bidders and a set $M$ of $m$ items, the outcomes of $\Omega$ correspond to $n$-vectors $S_1,…,S_n$, with $S \subseteq M$ denoting the buddle allocated to bidder $i$, with no item allocated twice. There are $(n+1)^m$ different outcomes. Each bidder $i$ has a private valutaion $v_i(S)$ for each bundle $S \subseteq M$ of items she might get. Thus, each bidder has $2^m$ private parameters.
Theorem: Muti-Parameter Welfare Maximization
In every general mechanism design enviroment, there is a DSIC welfare-maximizing mechanism.
Applying Two-Step approach allocation/payment rule design,
Allocation Rule
The first step. Assume agents truthfully report their private value, for welfare maximization, the only soluction to pick welfare-maximizing outcome, using bids as proxies for the unknown valuations. Given reports $\bf b_1, …, \bf b_n$, where each report $\bf b_i$ is now a vector indexed by $\omega$, define the allocation rule $\bf x$ by
已分配函数的角度看, 上式也被定义为 Allocative Efficency (AE). 注意这里用的公式是以机制设计体系下的形式化, 和上下文存在区别. We say that a social choice function $f(\cdot)=(k(\cdot), t_1(\cdot),…,t_n(\cdot))$ ia allocatively efficient if for each $\theta \in \Theta$, $k(\theta)$ satifies the following condition
The second step. Define the allocation rule, when coupled with above allocation rule, yield a DSIC mechanism.
这时候的困难在于Myerson引理失效, 因为在多维report下的单调性都很难定义, 且在0-1单参数环境下的crucial bid在多参数下没有类似的性质; 所以必须引出一个新思路定义payment rule.
Payment Rule 支付规则
The key idea is to generalize an alternative characterization of an agent $i$’s payment in a DISC welfare-maximizing mechanism, as the “externality” caused by $i$ — the welfare loss inflicted on other $n-1$ agents by $i$’s presence.
设计支付规则的关键思路: 刻画 agent $i$ 在DISC的社会福利最大化机制下的支付: 因agent $i$ 的导致的外部性, 即 agent $i$ 出现导致 [其他 agent 集体] 的社会福利损失.
因此形式化该思路下支付公式为
where $w^{\ast}=\bf x(\bf b)$ is the outcome chosen in above AE allocation rule. Intuitively, these payments force the agents to “internalize” their externalities, thereby aligning their incentives with those of a welfare-maximizing decision maker.
直觉上看, 上述支付规则迫使 agent [内部化他的外部性], 因此使得他们的动机和社会福利最大化保持一致.
In a single item auction, the winning bidder inflicts a welfare loss on the others equal to the second-highest bid (assuming truthful bids), and this is precisely the payment rule of a second-price auction.
回顾单商品二价auction, 胜出者造成的其他agent的社会福利损失正好和二价相等: 此时VCG支付规则公式的第一项正好为二价, 第二项为 0, 因此支付正好等于二价;
For an alternative interpretation of payments in the VCG mechanism, write the payment rule as
therefore think of agent $i$’s payment as her bid minis a “rebate”, this rebate equal to the increase in welfare attribute to $i$’s presence.
另一种 VCG 支付规则的解释: 智能体$i$的支付视为她的竞价减去一部分”退款”, 其中退款等于因 $i$ 的存在而产生的社会福利的增量; 按照这种解释, 在二价拍卖中, 竞价最高的竞拍者支付的竞价为
Proof of VCG DISC VCG 机制满足 DSIC 的证明
To verify the DSIC, we need show that for every agent $i$, and every set $b{-i}$ of reports by the other agents, agent $i$ maximizes her quasilinear utility $v_i(\bf x(\bf b))-p_i(\bf b)$ by setting $\bf b_i=\bf v_i$. Fix $i$ and $\bf b{-i}$ when chosen outcome $\bf x(\bf b)$ is $\omega^{\ast}$, we use vcg payment rule to rewrite $i$’s utiliy as
The term B is constant, independent of $i$’s report $\bf b_i$.
So the problem of maximizing agent $i$’s utility reduces to the problem of maximizing the first term A. As a thought experiment, suppose the agent $i$ has the power to choose the outcome $\omega^{\ast}$ directly, rather than merely influencing the chosen outcome indirectly via her choice of bid $\bf b_i$. Agent $i$ would, of course, use this extra power to choose an outcome that maximize the term A. If agent $i$ sets $\bf b_i=\bf v_i$, then the function
that the mechanism maximizes become identical to the term A that the agent wants to maximized. Thus, truthful reporting coaxes the mechanism to choose an outcome that maximizes agent $i$’s utility; no other report can be better.
假设 agent 能选择结果 $\omega^{\ast}$, 而不需要通过竞价来影响最终的结果, 那么他一定选择一个能最大化 A 项的结果, 现在 agent 选择 $\bf b_i=\bf v_i$, 那么机制要最大化的上式就和 agent 要最大化的A项一致了. 因此真实竞价可以”诱导”机制去选择最大化智能体 $i$ 效用的结果, 而任何其他报价都不能比这做的更好
Reference
[1]. Game Theory and Mechanism Design. Y Narahari.
[2]. Twenty Lectures on Algorithmic Game Theory. Tim Roughgarden.
转载请注明来源 goldandrabbit.github.io